Paper:
Refraction-Based Bundle Adjustment for Scale Reconstructible Structure from Motion
Akira Shibata*,**, Yukari Okumura*, Hiromitsu Fujii*,***, Atsushi Yamashita*, and Hajime Asama*
*The University of Tokyo
7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8654, Japan
**Ricoh Co., Ltd.
2-7-1 Izumi, Ebina-City, Kanagawa 243-0460, Japan
***Chiba Institute of Technology
2-17-1 Tsudanuma, Narashino, Chiba 275-0016, Japan
Structure from motion is a three-dimensional (3D) reconstruction method that uses one camera. However, the absolute scale of objects cannot be reconstructed by the conventional structure from motion method. In our previous studies, to solve this problem by using refraction, we proposed a scale reconstructible structure from motion method. In our measurement system, a refractive plate is fixed in front of a camera and images are captured through this plate. To overcome the geometrical constraints, we derived an extended essential equation by theoretically considering the effect of refraction. By applying this formula to 3D measurements, the absolute scale of an object could be obtained. However, this method was verified only by a simulation under ideal conditions, for example, by not taking into account real phenomena such as noise or occlusion, which are necessarily caused in actual measurements. In this study, to robustly apply this method to an actual measurement with real images, we introduced a novel bundle adjustment method based on the refraction effect. This optimization technique can reduce the 3D reconstruction errors caused by measurement noise in actual scenes. In particular, we propose a new error function considering the effect of refraction. By minimizing the value of this error function, accurate 3D reconstruction results can be obtained. To evaluate the effectiveness of the proposed method, experiments using both simulations and real images were conducted. The results of the simulation show that the proposed method is theoretically accurate. The results of the experiments using real images show that the proposed method is effective for real 3D measurements.
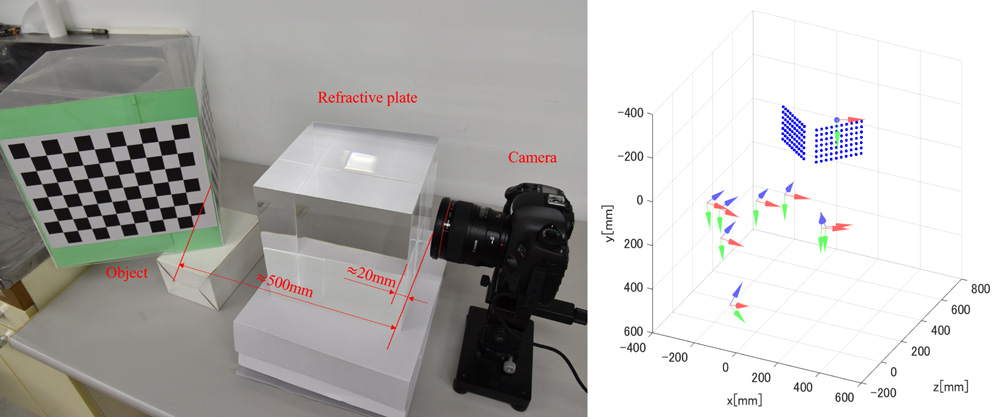
Scale reconstructible SfM system using refraction
- [1] H. C. Longuet-Higgins, “A Computer Algorithm for Reconstructing a Scene from Two Projections,” Nature, Vol.293, pp. 133-135, 1981.
- [2] C. Tomasi and T. Kanade, “Shape and Motion from Image Streams under Orthography: a Factorization Method,” Int. J. of Computer Vision, Vol.9, No.2, pp. 137-154, 1992.
- [3] R. I. Hartley, “In Defense of the Eight-Point Algorithm,” IEEE Trans. on Pattern Analysis and Machine Intelligence, Vol.19, No.6, pp. 580-593, 1997.
- [4] D. Nister, “An Efficient Solution to the Five-Point Relative Pose Problem,” IEEE Trans. on Pattern Analysis and Machine Intelligence, Vol.26, No.6, pp. 756-770, 2004.
- [5] M. Tomono, “3-D Localization and Mapping Using a Single Camera Based on Structure-from-Motion with Automatic Baseline Selection,” Proc. of the 2005 IEEE Int. Conf. on Robotics and Automation, pp. 3342-3347, 2005.
- [6] R. Kawanishi, A. Yamashita, T. Kaneko, and H. Asama, “Parallel Line-Based Structure from Motion by Using Omnidirectional Camera in Textureless Scene,” Advanced Robotics, Vol.27, No.1, pp. 19-32, 2013.
- [7] A. J. Davison, I. D. Reid, N. D. Molton, and O. Stasse, “MonoSLAM: Real-Time Single Camera SLAM,” IEEE Trans. on Pattern Analysis and Machine Intelligence, Vol.29, No.6, pp. 1052-1067, 2007.
- [8] T. Suzuki, Y. Amano, T. Hashizume, and S. Suzuki, “3D Terrain Reconstruction by Small Unmanned Aerial Vehicle Using SIFT-Based Monocular SLAM,” J. Robot. Mechatron., Vol.23, No.2, pp. 292-301, 2011.
- [9] N. Takeishi and T. Yairi, “Visual Monocular Localization, Mapping, and Motion Estimation of a Rotating Small Celestial Body,” J. Robot. Mechatron., Vol.29, No.5, pp. 856-863, 2017.
- [10] Z. Chai and T. Matsumaru, “ORB-SHOT SLAM: Trajectory Correction by 3D Loop Closing Based on Bag-of-Visual-Words (BoVW) Model for RGB-D Visual SLAM,” J. Robot. Mechatron., Vol.29, No.2, pp. 365-380, 2017.
- [11] R. A. Newcombe, S. J. Lovegrove, and A. J. Davison, “DTAM: Dense Tracking and Mapping in Real-Time,” Proc. of the 2009 IEEE Int. Conf. on Computer Vision, pp. 2320-2327, 2011.
- [12] C. Forster, M. Pizzoli, and D. Scaramuzza, “SVO: Fast Semi-Direct Monocular Visual Odometry,” Proc. of the 2014 IEEE Int. Conf. on Robotics and Automation, pp. 15-22, 2014.
- [13] R. I. Hartley and A. Zisserman, Multiple View Geometry in Computer Vision, Cambridge University Press, Second Edition, 2004.
- [14] D. Scaramuzza, F. Fraundorfer, M. Pollefeys, and R. Siegwart, “Absolute Scale in Structure from Motion from a Single Vehicle Mounted Camera by Exploiting Nonholonomic Constraints,” Proc. of the 2009 IEEE Int. Conf. on Computer Vision, pp. 1413-1419, 2009.
- [15] A. Shibata, H. Fujii, A. Yamashita, and H. Asama, “Scale-Reconstructable Structure from Motion Using Refraction with a Single Camera,” Proc. of the 2015 IEEE Int. Conf. on Robotics and Automation, pp. 5239-5244, 2015.
- [16] A. Shibata, H. Fujii, A. Yamashita, and H. Asama, “Absolute Scale Structure from Motion Using a Refractive Plate,” Proc. of the 2015 IEEE/SICE Int. Symp. on System Integration (SII2015), pp. 540-545, 2015.
- [17] Y. Okumura, H. Fujii, A. Yamashita, and H. Asama, “Global Optimization with Viewpoint Selection for Scale-reconstructible Structure from Motion Using Refraction,” Proc. of the Int. Workshop on Advanced Image Technology 2017 (IWAIT2017), 2017.
- [18] A. Jordt-Sedlazeck and R. Koch, “Refractive Structure-from-Motion on Underwater Images,” Proc. of the 2013 IEEE Int. Conf. on Computer Vision, pp. 57-64, 2013.
- [19] T. Treibitz, Y. Y. Schechner, C. Kuntz, and H. Singh, “Flat Refractive Geometry,” IEEE Trans. on Pattern Analysis and Machine Intelligence, Vol.34, No.1, pp. 51-65, 2012.
- [20] Y. Chang and T. Chen, “Multi-View 3D Reconstruction for Scenes under the Refractive Plane with Known Vertical Direction,” Proc. of the 2011 IEEE Int. Conf. on Computer Vision, pp. 351-358, 2011.
- [21] A. Agrawal, S. Ramalingam, Y. Taguchi, and V. Chari, “A Theory of Multi-Layer Flat Refractive Geometry,” Proc. of the 2012 IEEE Conf. on Computer Vision and Pattern Recognition, pp. 2316-2323, 2012.
- [22] D. H. Lee, I. S. Kweon, and R. Cipolla, “A Biprism-Stereo Camera System,” Proc. of the 1999 IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, Vol.1, pp. 82-87, 1999.
- [23] A. Yamashita, Y. Shirane, and T. Kaneko, “Monocular Underwater Stereo – 3D Measurement Using Difference of Appearance Depending on Optical Paths –,” Proc. of the 2010 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, pp. 3652-3657, 2010.
- [24] Z. Chen, K. K. Wong, Y. Matsushita, X. Zhu, and M. Liu, “Self-Calibrating Depth from Refraction,” Proc. of the 2011 IEEE Int. Conf. on Computer Vision, pp. 635-642, 2011.
- [25] C. Gao and N. Ahuja, “A Refractive Camera for Acquiring Stereo and Super-resolution Images,” Proc. of the 2006 IEEE Computer Society Con. on Computer Vision and Pattern Recognition, pp. 2316-2323, 2006.
- [26] N. Snavely, S. M. Seitz, and R. Szeliski, “Photo Tourism: Exploring Photo Collections in 3D,” ACM Trans. on Graphics, Vol.25, pp. 835-846, 2006.
- [27] S. Agarwal, Y. Furukawa, N. Snavely, I. Simon, B. Curless, S. M. Seitz, and R. Szeliski, “Building Rome in a Day,” Communications of the ACM, Vol.54, No.10, pp. 105-112, 2011.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.