Paper:
Control Parameters Tuning Method of Nonlinear Model Predictive Controller Based on Quantitatively Analyzing
Tomohiro Henmi
Department of Electro-Mechanical Engineering, National Institute of Technology, Kagawa College
355 Chokushicho, Takamatsu, Kagawa 761-8058, Japan
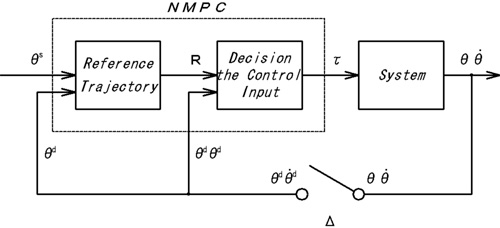
ANMPC controller
- [1] J. K. Maciejowski, “Predictive Control with Constraints,” Prentice Hall, New Jersey, 2002.
- [2] W. H. Kwon and A. E. Pearson, “On Feedback Stabilization of Time-Varying Discrete Linear Systems,” IEEE Trans. Autom. Control, Vol.23, pp. 479-481, 1978.
- [3] V. H. L. Cheng, “A Direct Way to Stabilize Continuous-Time and Discrete-Time Linear Time-Varying Systems,” IEEE Trans. Autom. Control, Vol.24, pp. 641-643, 1979.
- [4] C. C. Chen and L. Shaw, “On Receding Horizon Feedback Control,” Automatica, Vol.18, pp. 349-352, 1982.
- [5] T. Henmi, T. Ohta, M. Deng, and A. Inoue, “Tracking Control of The Two-link Manipulator using Nonlinear Model Predictive Control,” Proc. of IEEE Int. Conf. on Networking, Sensing and Control, pp. 761-766, 2009.
- [6] T. Henmi, M. Deng, and A. Inoue, “Adaptive Control of a Two-link Planar Manipulator using Nonlinear Model Predictive Control,” Proc. of 2010 IEEE Int. Conf. on Mechatronics and Automation, pp. 1868-1873, 2010.
- [7] S. Jung and T. Wen, “Nonlinear Model Predictive Control for Swing-UP of a Rotary Inverted Pendulum,” Trans. of the ASME, Vol.126, pp. 666-673, 2004.
- [8] D. Q. Mayne and H. Michalska, “Receding Horizon Control of Nonlinear System,” IEEE Trans. Autom. Control, Vol.35, pp. 814-824, 1990.
- [9] T. Kobayashi and T. Tani, “Application of Cooperative Control to Petroleum Plants Using Fuzzy Supervisory Control and Model Predictive Multi-variable Control,” J. of Advanced Computational Intelligence and Intelligent Informatics, Vol.5, No.6, pp. 333-337, 2001.
- [10] T. Kayahara and T. Henmi, “Anti-windup compensator for nonlinear model predictive control,” Proc. of 2012 Int. Conf. on Advanced Mechatronic Systems, pp. 406-411, 2012.
- [11] A. Matsushita and T. Henmi, “The Performance Validation of an Actuator Fault Detection of a Nonlinear Model Predictive Controller in using Approximate Differentiation,” Proc. of 5th Int. Symposium on Advanced Control of Industrial Processes, pp. 397-402, 2014.
- [12] S. Watanabe and M. Harada, “Optimal Tracking Control of a Micro Ground Vehicle,” J. of Robotics and Mechatronics, Vol.27, No.6, pp. 653-659, 2015.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.