Top > JRM > A New Method to Solve the Kinematic Problems of Parallel Robot ...

single-rb.php

JRM Vol.28 No.3 pp. 404-417
doi: 10.20965/jrm.2016.p0404
(2016)

Paper:

Views over last 60 days: 2,012

A New Method to Solve the Kinematic Problems of Parallel Robots Using Generalized Reduced Gradient Algorithm

Thanh Trung Trang*, Wei Guang Li*, and Thanh Long Pham**

*School of Mechanical and Automotive Engineering, South China University of Technology
381 Wuhan Road, Tianhe District, Guangzhou, Guangdong 510641, China

**Faculty of Mechanical Engineering, Thai Nguyen University of Technology
3/2 Tich Luong Road, Thai Nguyen City, Thai Nguyen, Viet Nam

Received:
September 11, 2015
Accepted:
March 28, 2016
Published:
June 20, 2016
Creative Commons License
Keywords:
parallel robot, kinematic problem, equivalent structure, optimized problems, generalized reduced gradient algorithm
Abstract
This paper proposes a new method of solving the kinematic problems for parallel robots. The paper content aims to solve nonlinear optimization problems with constraints rather than to directly solve high-order nonlinear systems of equations. The nonlinear optimization problems shall be efficiently solved by applying the Generalized Reduced Gradient algorithm and appropriate downgrade techniques. This new method can be able to find exact kinematic solutions by assigning constraints onto the parameters. The procedure can be done without filtering control results from mathematical solution, from which the control time of manipulators can be reduced. The numerical simulation results in this paper shall prove that the method can be applied to solve kinematic problems for a variety of parallel robots regardless of its structures and degree of freedom (DOF). There are several advantages of the proposed method including its simplicity leading to a shorter computing time as well as achieving high accuracy, high reliability, and quick convergence in final results. Hence, the applicability of this method in solving kinematic problems for parallel manipulators is remarkably high.
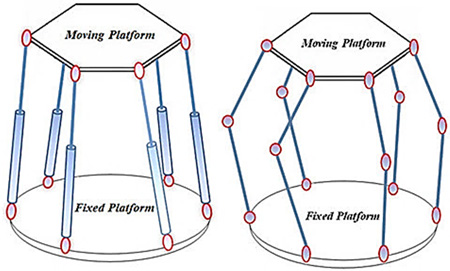
Stewart Gough robot and the equivalent substitutional configuration

Stewart Gough robot and the equivalent substitutional configuration

Cite this article as:
T. Trang, W. Li, and T. Pham, “A New Method to Solve the Kinematic Problems of Parallel Robots Using Generalized Reduced Gradient Algorithm,” J. Robot. Mechatron., Vol.28 No.3, pp. 404-417, 2016.
Data files:
References
  1. [1] D. Stewart, “A platform with Six Degrees of Freedom,” Proc.of the Inst. Mech. Eng. London, Part 1, Vol.180, No.5, pp. 371-386, 1965.
  2. [2] J. P. Merlet, “Direct kinematic of planar parallel manipulator,” Proc. IEEE Int. Conf. on Robotic and Automation, pp. 3744-3749, 1996.
  3. [3] S. Kucuk, “Kinematics, singularity and dexterity analysis of planar parallel manipulators based on DH method,” Robot Manipulators New Achievements, InTech, pp. 387-400, 2010.
  4. [4] M. Dehghani, M. Ahmadi, A. Khayatian, and M. Eghtesad, “Wavelet Based Neural Network Solution for Forward Kinematics Problem of HEXA Parallel Robot,” Int. Conf. on Intelligent Engineering Systems, INES 2008, pp. 63-70, 2008.
  5. [5] K. V. Varalakshmi and Dr. J. Srinivas, “Stiffness Metrics for Design of 3-RRR Flexible Manipulator,” Int. J. of Modern Engineering Research, Vol.2, No.4, pp. 2021-2027, 2012.
  6. [6] M. Raghavan and B. Roth, “Solving polynomial systems for the kinematic analysis and synthesis of mechanisms and robot manipulators,” Trans. ASME, Vol.117, pp. 71-79, 1995.
  7. [7] R. Parrish, E. Dieudonné, and R. Bardusch, “An actuator extension transformation for a motion simulator and an inverse transformation applying newton-raphson’s method,” Technical report D-7067, NASA, 1972.
  8. [8] R. Boudreau and N. Turkkan, “Solving the forward kinematics of parallel manipulators with a genetic algorithm,” J. of Robotics Systems, Vol.13, No.2, pp. 111-125, 1995.
  9. [9] A. Omran, M. Bayoumi, A Kassem, and G. El-Bayoumi, “Optimal Forward Kinematics Modeling of Stewart Manipulator Using Genetic Algorithms,” Jordan J. of Mechanical and Industrial Engineering, Vol.3, No.4, pp. 280-293, 2009.
  10. [10] T. J. Ypma, “Historical development of the newton-raphson method,” SIAM Rev., Vol.37, No.4, pp. 531-551, 1995.
  11. [11] R. Chandra and L. Rolland, “On solving the Forward Kinematics of the 3RPR Planar Parallel Manipulator using a Hybrid Meta-Heuristic,” Applied Mathematics and Computation, Vol.217, No.22, pp. 8997-9008, 2011.
  12. [12] J. P. Merlet, “Solving the forward kinematics of a Gough-type parallel manipulator with interval analysis,” Int. J. Robot. Res., Vol.23, No.3, pp. 221-236, 2004.
  13. [13] D. Chablat, P. Wenger, and J. P. Merlet, “Workspace analysis of the orthoglide using interval analysis,” Proc. of ARK, pp. 397-406, 2002.
  14. [14] K. Waldron, P. Nanua, and V. Murthy, “Direct kinematic solution of a Stewart platform,” Proc. of Int. Conf. on Robotics and Automation, Vol.6, No.4, pp. 438-444, 1990.
  15. [15] T. Y. Lee and J. K. Shim, “Forward kinematics for the general 6- 6 Stewart platform using algebraic elimination,” Mech. Theory, Vol.36, pp. 1073-1085, 2002.
  16. [16] S. V. Sreenivasan and P. Nanua, “Solution of the direct position kinematics problem of the general stewart platform using advanced polynomial continuation,” Proc. of 22nd Biennial Mechanisms Conf., pp. 99-106, 1992.
  17. [17] M. Raghavan, “The Stewart platform of general geometry has 40 configurations,” ASME J. of Mech. Design, Vol.15, pp. 277-282, 1993.
  18. [18] J. P. Merlet, “Direct kinematics of parallel manipulators,” IEEE Trans. on Robotics and Automation, Vol.9, No.2, pp. 842-846, 1993.
  19. [19] Y. Wang, “A direct numerical solution to forward kinematics of general Stewart–Gough platforms,” J. of Robotica, Vol.25, No.1, pp. 121-128, 2007.
  20. [20] L. Baron and J. Angeles, “The direct kinematics of parallel manipulators under joint sensor redundancy,” IEEE conf. Trans. Robot. Autom., Vol.16, No.1, pp. 12-19, 2000.
  21. [21] P. T. Long and H. Vi, “Determine the value of the control variable kinematic Robot,” Viet Nam J. of Mechanic, Vol.65, pp. 31-34, 2008.
  22. [22] P. T. Long, “A New Method to Solve the Reverse Kinematic Robot Problem,” ISTS Swissotel Le Concorde, pp. 43-46, 2012.
  23. [23] B. Dasgupta and T. S. Mruthyunjaya, “A constructive predictor-corrector algorithm for the direct position kinematic problem for a general 6-6 stewart platform,” Mechanism Machine Theory, Vol.31, pp. 799-811, 1996.
  24. [24] M. Husty, “An algorithm for solving the direct kinematic of Stewart-Gough-type platforms,” Mechanism Machine Theory, Vol.31, pp. 365-379, 1996.
  25. [25] L. Rolland, “Outils algébriques pour la résolution de problèmes géométriques et l’analyse de trajectoire de robots parallèles prévus pour des applications à haute cadence et grande précision,” Ph.D. thesis, Université Henri Poincaré, 2003.
  26. [26] J. P. Merlet, “Parallel manipulators, part 1: Theory; design, kinematics, dynamics and control,” Technical report 646, INRIA, Sophia-Antipolis, 1987.
  27. [27] F. Faluyi and C. Arum, “Design Optimization of Plate Girder Using Generalized Reduced Gradient and Constrained Artificial Bee Colony Algorithms,” Int. J. of Emerging Technology and Advanced Engineering, Vol.2, Issue 7, 2012.
  28. [28] L. Yan and D. Ma, “Global Optimization for constrained nonlinear programs using line-up competition algorithm,” Compus. Oper. Res., Vol.25, No.11-22, pp. 1601-1610, 2001.
  29. [29] L. S. Lasdon, A. D. Warren, A. Jain, and M. Ratner, “Design and Testing of a generalized reduced gradient code for nonlinear Programming,” ACM Trans. Math. SoftWare, Vol.4, No.1, pp. 34-50, 1978.
  30. [30] C. Kao, “Performance of Several nonlinear programming software packages on microcomputers,” Comput. Oper. Res., Vol.25, No.10, pp. 807-816, 1998.
  31. [31] D. Jagobovic, “Ocjena ucinkovitosti postupaka za rjesavanje kinematike Stewartowih paralelnih mehanizama,” MAGISTARSKI RAD, zagreb 2001, pp. 81-95, 2001.

Creative Commons License  This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.

*This site is desgined based on HTML5 and CSS3 for modern browsers, e.g. Chrome, Firefox, Safari, Edge, Opera.

Last updated on Apr. 22, 2024