Paper:
Numerical Investigation on Transverse Maneuverability of a Vectored Underwater Vehicle Without Appendage
Rongmin Zhang, Yuan Chen†, and Jun Gao
School of Mechanical, Electrical & Information Engineering, Shandong University at Weihai
Wenhuaxilu 180, Weihai 264209, China
†Corresponding author
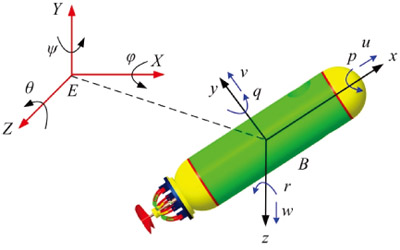
Solid model of a vectored underwater vehicle
- [1] T. Naruse, “Development of Bottom-Reliant Type Underwater Robots,” J. of Robotics and Mechatronics, Vol.26, No.3, pp. 279-286, 2014.
- [2] C. Shili, W. Min, Li. Yibo et al., “Steering Control Strategy of AUV with Vectored Thruster Based on Double-Loop Mode,” J. of Tianjin University, Vol.47, No.6, pp. 530-534, 2014.
- [3] F. Takemura, S. Futenma, K. Kawabata et al., “Experimental Verification of Lifting Force of Underwater Robot with Thrusters Using Passive Posture Maintenance,” J. of Robotics and Mechatronics, Vol.25, No.5, pp. 812-819, 2013.
- [4] Z. Rongmin, C. Yuan, and G. Jun, “Dynamic Analysis of Decoupled Spherical Parallel Mechanism for Vectored Thruster,” Trans. of the Chinese Society for Agricultural Machinery, Vol.46, No.6, pp. 319-326, 2015.
- [5] X. Feng, Z. Zaojian, Y. Jianchuan et al., “Identification modeling of underwater vehicles’ nonlinear dynamics based on support vector machines,” Ocean Engineering, Vol.67, pp. 68-76, 2013.
- [6] B. Xin, L. Xiaohui, and S. Zhaocun, “A vectored water jet propulsion method for autonomous underwater vehicles,” Ocean Engineering, Vol.74, pp. 133-140, 2013.
- [7] W. Shuxin, L. Fang, S. Shuai et al., “Dynamic Modeling of Hybrid Underwater Glider Based on the Theory of Differential Geometry and Sea Trails,” Chinese J. of Mechanical Engineering, Vol.50, No.2, pp. 19-27, 2014.
- [8] V. Kopman, N. Cavaliere, and M. Porfiri, “MASUV-1:A Miniature Underwater Vehicle With Multidirectional Thrust Vectoring for Safe Animal Interactions,” IEEE/ASME Trans. on Mechatronics, Vol.17, No.3, pp. 563-571, 2012.
- [9] P. Jinmo and K. Nakwan, “Dynamics modeling of a semi-submersible autonomous underwater vehicle with a towfish towed by a cable,” Int. J. of Naval Architecture and Ocean Engineering, Vol.7, No.2, pp. 409-425, 2015.
- [10] L. Guijie, C. Gong, J. Jianbo et al., “Dynamics modeling and control simulation of an autonomous underwater vehicle,” J. of Coastal Research, Vol.73, pp. 741-746, 2015.
- [11] W. Chuanfeng, Z. Fumin, and D. Schaefer, “Dynamic modeling of an autonomous underwater vehicle,” J. of Marine Science and Technology, Vol.20, No.2, pp. 199-212, 2015.
- [12] G. A. Elnashar, “Dynamics modeling, performance evaluation and stability analysis of an autonomous underwater vehicle,” Int. J. of Modeling, Identification and Control, Vol.21, No.3, pp. 306-320, 2014.
- [13] W. Yanhui, D. Zhenzhen, C. Wei et al., “Dynamic modeling for multi-wing autonomous underwater vehicle motion control system,” J. of Huazhong University of Science and Technology (Natural Science Edition), Vol.43, No.6, pp. 106-111, 2015.
- [14] Z. Baoqiang, W. Xiaohao, Y. Baoheng et al., “Lyapunov stability analysis of the underwater glider,” J. of Harbin Engineering University, Vol.36, No.1, pp. 83-87, 2015.
- [15] Z. Xiaoyu, H. Yuntao, B. Tao et al., “H-infinity controller design using LMIs for high-speed underwater vehicles in presence of uncertainties and disturbances,” Ocean Engineering, Vol.104, pp. 359-369, 2015.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.