Paper:
Optimal Tracking Control of a Micro Ground Vehicle
Soichiro Watanabe and Masanori Harada
National Defense Academy of Japan
1-10-20 Hashirimizu, Yokosuka, Kanagawa 239-8686, Japan
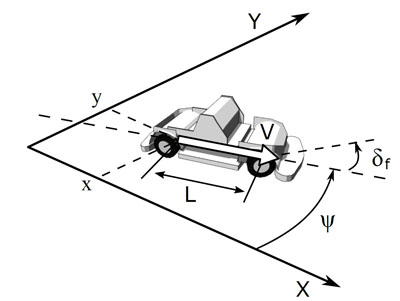 Coordinate system of MGV
Coordinate system of MGV- [1] T. Kobayashi and S. Majima, “Automatic Parking Control for a 4-Wheeled Vehicle by Non-Linear Receding Horizon Control,” Trans. of Japan Society of Mechanical Engineers, Series C, Vol.70, No.695, pp. 166-173, 2004 (in Japanese).
- [2] M. Hurni, P. Sekhavat, and I. M. Ross, “Autonomous Trajectory Planning Using Real-Time Information Updates,” AIAA Guidance, Navigation and Control Conf., AIAA 2008-6305, 2008.
- [3] Q. Gong, L. R. Lewis, and I. M. Ross, “Pseudospectral Motion Planning for Autonomous Vehicles,” J. of Guidance, Control, and Dynamics, Vol.32, No.3, pp. 1039-1045, 2009.
- [4] S. Watanabe and M. Harada, “Optimal Guidance and Control of Micro Ground Vehicles,” Proc. of 2014 JSAE Annual Congress (spring), No.40-14, pp. 15-20, 2014 (in Japanese).
- [5] J. M. Maciejowski, “Predictive Control with Constraints,” Pearson Education Limited, 2002 (S. Adachi and M. Kanno (Trans.), “Predictive Control with Constraints,” Tokyo Denki University Press, 2005 (in Japanese)).
- [6] T. Ohtsuka (Ed.), “Practical Application of Control by Real-Time Optimization,” Corona Publishing, 2015 (in Japanese).
- [7] K. Oyama and K. Nonaka, “Model Predictive Parking Control for Nonholonomic Vehicles using Time-State Control Form,” 2013 European Control Conf., pp. 458-465, 2013.
- [8] K. Oyama and K. Nonaka, “Model Predictive Parking Control with Obstacle Avoidance Considering Automatic Tuning of Switching Point,” Trans. of the Society of Instrument and Control Engineers, Vol.50, No.1, pp. 9-17, 2014 (in Japanese).
- [9] S. Watanabe and M. Harada, “Real-Time Optimal Feedback Control of UGVs Using Modified Carathéodory-π Solutions,” Proc. of 12th Int. Symposium on Advanced Vehicle Control, CD-ROM, pp. 385-390, 2014.
- [10] A. E. Bryson and Y. C. Ho, “Applied Optimal Control,” Taylor& Francis, Levittown, 1975.
- [11] J. Z. Ben-Asher, “Optimal Control Theory with Aerospace Applications,” AIAA Education Series, Virginia, 2010.
- [12] M. Harada, “Direct Trajectory Optimization by a Jacobi Pseudospectral Method with the Weights of High-Order Gauss-Lobatto Formulae,” Trans. of Japan Society of Mechanical Engineers, Series C, Vol.73, No.728, pp.119-124, 2007 (in Japanese).
- [13] M. Harada, “Covector Estimation for Optimal Control Solver using a Jacobi Pseudospectral Method,” Trans. of the Society of Instrument and Control Engineers, Vol.49, No.8, pp. 808-815, 2013 (in Japanese).
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.