Paper:
Parameter Tuning in the Application of Stochastic Resonance to Redundant Sensor Systems
Nagisa Koyama, Shuhei Ikemoto, and Koh Hosoda
Graduate School of Engineering Science, Osaka University
1-3 Machikaneyama, Toyonaka, Osaka 560-8531, Japan
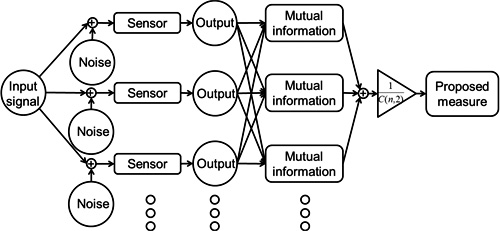
Basic concept of proposed method
- [1] R. Benzi, A. Sutera, and A. Vulpiani, “The mechanism of stochastic resonance,” J. Phys. A: Mathemat. Gen., Vol.14, pp. 453-457, 1981.
- [2] D. Russell, L. Wilkens, F. Moss et al., “Use of behavioural stochastic resonance by paddle fish for feeding,” Nature, Vol.402, No.6759, pp. 291-293, 1999.
- [3] J. K. Douglass, L. Wilkens, E. Pantazelou, and F. Moss, “Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance,” Nature, Vol.365, pp. 337-340, 1993.
- [4] J. Collins, T. Imhoff, and P. Grigg, “Noise-enhanced information transmission in rat SA1 cutaneous mechanoreceptors via aperiodic stochastic resonance,” J. of Neurophysiology, Vol.76, No.1, pp. 642-645, 1996.
- [5] J. Collins, T. Imhoff, and P. Grigg, “Noise-enhanced tactile sensation,” Nature, Vol.383, No.31, p. 770, 1996.
- [6] J. B. Fallon and D. L. Morgan, “Fully Tuneable Stochastic Resonance in Cutaneous Receptors,” J. Nourophysiol., Vol.94, pp. 928-933, 2005.
- [7] M. Ohka and S. Kondo, “Stochastic resonance aided tactile sensing,” Robotica, Vol.27, No.04, pp. 633-639, 2009.
- [8] Y. Kurita, M. Shinohara, and J. Ueda, “Wearable sensorimotor enhancer for a fingertip based on stochastic resonance,” 2011 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 3790-3795, 2011.
- [9] A. Bulsara and A. Zador, “Threshold detection of wideband signals: A noise-induced maximum in the mutual information,” Physical Review E, Vol.54, No.3, pp. 2185-2188, 1996.
- [10] T. Munakata, A. Sato, and T. Hada, “Stochastic Resonance in a Simple Threshold System from a Static Mutual Information Point of View,” J. of the Physical Society of Japan, Vol.74, No.7, pp. 2094-2098, 2005.
- [11] L. Gammaitoni, P. Hänggi, P. Jung, and F. Marchesoni, “Stochastic resonance,” Reviews of Modern Physics, Vol.70, No.1, pp. 223-287, 1998.
- [12] J. Collins, C. Chow, and T. Imhoff, “Aperiodic stochastic resonance in excitable systems,” Physical Review E, Vol.52, No.4, pp. 3321-3324, 1995.
- [13] K. Wiesenfeld, F. Moss et al., “Stochastic resonance and the benefits of noise: from ice ages to crayfish and SQUIDs,” Nature, Vol.373, No.6509, pp. 33-36, 1995.
- [14] C. Bishop and S. S. En Ligne, “Pattern recognition and machine learning,” Vol.4, springer New York, 2006.
- [15] M. Matsumoto and T. Nishimura, “Mersenne twister: a 623-dimensionally equidistributed uniform pseudo-random number generator,” ACM Trans. on Modeling and Computer Simulation (TOMACS), Vol.8, No.1, pp. 3-30, 1998.
- [16] G. Marsaglia, “Xorshift rngs,” J. of Statistical Software, Vol.8, No.14, pp. 1-6, 2003.
- [17] C. Igel and M. Hüusken, “Empirical evaluation of the improved Rprop learning algorithms,” Neurocomputing, Vol.50, No.105-123, 2003.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.