Paper:
Model-Based Footstep Planning Method for Biped Walking on 3D Field
Daiki Kobayashi, Tomohito Takubo, and Atsushi Ueno
Graduate School of Engineering, Osaka City University
3-3-138 Sugimoto Sumiyoshi-ku, Osaka 558-8585, Japan
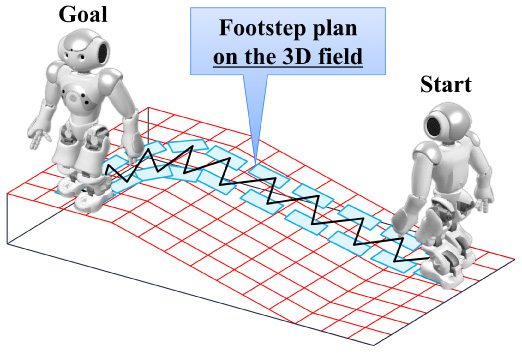 Footstep planning on the 3D field
Footstep planning on the 3D field- [1] J. S. Hu, J. H. Cheng, and Y. J. Chang, “Spatial Trajectory Tracking Control of Omni-directional Wheeled Robot Using Optical Flow Sensor,” Proc. of IEEE Int. Conf. on Control Applications, pp. 1462-1467, 2007.
- [2] E. Maalouf, M. Saad, and H. Saliah, “A Higher Level Path Tracking Controller for a Four-wheel Differentially Steered Mobile Robot,” Robotics and Autonomous Systems. Vol.54, Issue 1, pp. 23-33, 2006.
- [3] J. Kuffner, K. Nishiwaki, S. Kagami, M. Inaba, and H. Inoue, “Footstep Planning Among Obstacles for Biped Robots,” Proc. of IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, Vol.1, pp. 500-505, 2001.
- [4] R. Kurazume, T. Hasegawa, and K. Yoneda, “The Sway Compensation Trajectory for a Biped Robot,” Proc. of IEEE Int. Conf. on Robotics and Automation, Vol.1, pp. 925-931, 2003.
- [5] K. Nishiwaki, S. Kagami, J. Kuffner, M. Inaba, and H. Inoue, “Online Humanoid Walking Control System and a Moving Goal Tracking Experiment,” Proc. of IEEE Int. Conf. on Robotics and Automation, Vol.1, pp. 911-916, 2003.
- [6] H. Kobayashi and T. Sugihara, “Self-consistent Automatic Navigation of COM and Feet for Realtime Humanoid Robot Steering,” Proc. of IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, pp. 3525-3530, 2009.
- [7] J. Chestnutt, M. Lau, G. Cheung, J. Kuffner, J. Hodgins, and T. Kanade, “Footstep Planning for the Honda ASIMO Humanoid,” Proc. of IEEE Int. Conf. on Robotics and Automation, pp. 629-634, 2005.
- [8] J. Garimort, A. Hornung, and M. Bennewitz, “Humanoid Navigation with Dynamic Footstep Plans,” Proc. of IEEE Int. Conf. on Robotics and Automation, pp. 3982-3987, 2011.
- [9] W. Huang, J. Kim, and C. G. Atkeson, “Energy-based Optimal Step Planning for Humanoids,” Proc. of IEEE Int. Conf. on Robotics and Automation, pp. 3109-3114, 2013.
- [10] O. Kanoun, E. Yoshida, and J.-P. Laumond, “An Optimization Formulation for Footsteps Planning,” Proc. of IEEE-RAS Int. Conf. on Humanoid Robots, pp. 202-207, 2009.
- [11] O. Kanoun, J.-P. Laumond, and E. Yoshida, “Planning Foot Placements for a Humanoid Robot: A Problem of Inverse Kinematics,” Int. J. of Robotics Research, Vol.30, Issue 4, pp. 476-485, 2011.
- [12] N. Yao, T. Takubo, K. Ohara, Y. Mae, and T. Arai, “Gait Planning for a Biped Robot by a Nonholonomic System with Difference Equation Constraints,” Proc. of IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, pp. 4471-4476, 2010.
- [13] D. Goldfarb and A. Idnani, “A Numerically Stable Dual Method for Solving Strictly Convex Quadratic Programs,” Mathematical Programming, Vol.27, Issue 1, pp. 1-33, 1983.
- [14] J. M. Maciejowski, “Predictive Control with Constraints,” Prentice Hall, 2002.
- [15] T. Sugihara, “Solvability-Unconcerned Inverse Kinematics by the Levenberg-Marquardt Method,” IEEE Trans. on Robotics, Vol.27, Issue 5, pp. 984-991, 2011.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.