Top > JRM > Analysis and Optimization for Balancing Mechanism of High-Spee ...

single-rb.php

JRM Vol.26 No.5 pp. 622-627
doi: 10.20965/jrm.2014.p0622
(2014)

Paper:

Views over last 60 days: 1,141

Analysis and Optimization for Balancing Mechanism of High-Speed & Heavy-Load Manipulators

Yongfei Xiao, Shuhui Bi, Xuelin Wang,
Xiangdong Li, and Xinjian Fan

Shandong Provincial Key Laboratory of Robot and Manufacturing Automation Technology, Institute of Automation, Shandong Academy of Science, No.19, Keyuan Road, Jinan, Shandong 250014, China

Received:
April 15, 2014
Accepted:
August 5, 2014
Published:
October 20, 2014
Creative Commons License
Keywords:
balancing mechanism, optimized design, payload capacity, dynamic model, nonlinear influence
Abstract
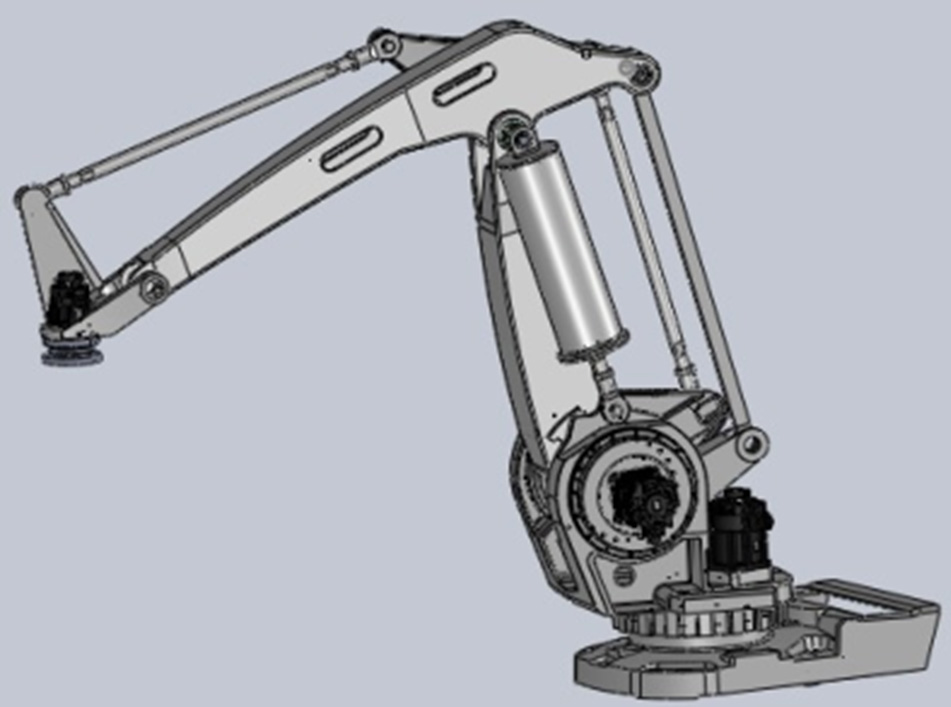Balancing mechanism of robots
Heavy-load manipulators usually have a balance to minimize energy consumption and maximize payload capacity. Appropriate design parameters are important to balancing devices in improving performance. We propose evaluating optimal parameters to achieve the best possible manipulator motion features. A dynamic manipulator model with a parallel-link mechanism is analyzed using the Lagrange principal. We also propose a way to reduce nonlinear influence while improving payload capacity. The optimized method is used for instructing how to design and optimize heavyload manipulators, as shown through simulation and experiments.
Cite this article as:
Y. Xiao, S. Bi, X. Wang, X. Li, and X. Fan, “Analysis and Optimization for Balancing Mechanism of High-Speed & Heavy-Load Manipulators,” J. Robot. Mechatron., Vol.26 No.5, pp. 622-627, 2014.
Data files:
References
  1. [1] Y.-B. Lu, C.-H. Zhao, L. Zhang, and J.-L. Liu, “The analysis and optimization for the balancing cylinder of industrial robot,” Develop & Innovation of Machinery & Electrical Products. China, Vol.24, pp. 19-20, 2011.
  2. [2] W. Yangnian and G. Clement, “Design of reactionless 3-DOF and 6-DOF parallel manipulators using parallelepiped mechanisms,” IEEE Trans. of Robotics, Vol.21, pp. 821-833, 2005.
  3. [3] H. Shen, “Optimization on the lower arm equilibrator of an arcwelding robot,” Modular Machine Tool & Automatic Manufacturing Technique, Vol.9, pp. 79-80, 2004.
  4. [4] X. Tang, W. Li, T. Zhang, and G. Tuo, “Effect of parallel four-bar mechanism on spotwelding robot,” J. of China Agricultural University, Vol.4, pp. 37-40, 2004.
  5. [5] J. L. Herder, “Design of spring force compensation systems,” Mechanism Mach. Theory, Vol.33, No.1, pp. 151-161, 1998.
  6. [6] A. Lecours and C. Gosselin, “Reactionless two-degree-of-freedom planar parallel mechanism with variable payload,” ASME J. Mechanisms Robot., Vol.2, No.4, pp. 041010-1–041010-7, 2010.
  7. [7] M. Arsenault and C. M. Gosselin, “Static balancing of tensegrity mechanisms,” ASME J. Mech. Design, Vol.129, No.3, pp. 295-300, 2007.
  8. [8] I. Simionescu and L. Ciupitu, “The static balancing of the industrial robot arms – Part II: Continuous balancing,” Mech. Mach. Theory, Vol.35, No.9, pp. 1299-1311, 2000.
  9. [9] C. M. Gosselin, F. Vollmer, G. Cote, and W. Yangnian, “Synthesis and design of reactionless three-degree-of-freedom parallel mechanisms,” IEEE Trans. of Robtics and Automation, Vol.20, pp. 191-199, 2004.
  10. [10] W. K. Chung and K. S. Cho, “On the dynamic characteristics of a balance PUMA-760 robot,” IEEE Trans. of Industrial Electronics, Vol.35, pp. 222-230, 1988.
  11. [11] Z.Wenhong, T. Lamarche, and P. Barnard, “Modular Robot Manipulators with Preloadable Modules,” ICMA 2007, Harbin, pp. 7-12, 2007.
  12. [12] L. Yanbo and K. E. Bekris, “Balancing state-space coverage in planning with dynamics,” 2010 IEEE Int. Conf. on Robotics and Automation, Alaska, pp. 3246-3253, 2010.
  13. [13] B. Liping, “Simulation analysis of robot dynamics based on ADAMS,” Mechanical and Electrical Engineering Magazine, Vol.24, pp. 75-77, 2007.

Creative Commons License  This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.

*This site is desgined based on HTML5 and CSS3 for modern browsers, e.g. Chrome, Firefox, Safari, Edge, Opera.

Last updated on Apr. 05, 2024