Top > JACIII > Lattice Based Communication P Systems

single-jc.php

JACIII Vol.27 No.6 pp. 1130-1136
doi: 10.20965/jaciii.2023.p1130
(2023)

Research Paper:

Views over last 60 days: 78

Lattice Based Communication P Systems

Junli Xu*, Xiyu Liu**, and Jie Xue** ORCID Icon

*School of Computer Science and Technology, Shandong Jianzhu University
No.1000 Fengming Road, Licheng District, Jinan 250101, China

**Business School, Shandong Normal University
No.88 East Wenhua Road, Lixia District, Jinan 250014, China

Received:
September 18, 2019
Accepted:
July 18, 2023
Published:
November 20, 2023
Creative Commons License
Keywords:
LTC-P systems, formal framework, computational power, SAT, HPP
Abstract

Lattice based communication P (LTC-P) systems are a class of extended P systems with lattice membrane structures. This new P-system is recently proposed in our work and LTC-P systems have been shown to be computational completeness. LTC-P systems can efficiently solve some kinds of combination-optimization problems. The purpose of this paper is to investigate the computation power of LTC-P systems through comparison with Chomsky families and Lindenmayer system. The formal framework of LTC-P systems is also provided. Then, we use LTC-P systems to solve SAT and HPP in linear time. Results have shown that LTC-P systems have comparative advantage in the use of membrane numbers.

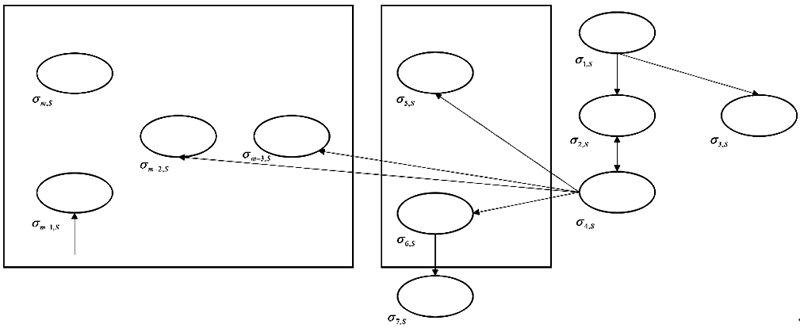
SN P systems of solving SAT problem

SN P systems of solving SAT problem

Cite this article as:
J. Xu, X. Liu, and J. Xue, “Lattice Based Communication P Systems,” J. Adv. Comput. Intell. Intell. Inform., Vol.27 No.6, pp. 1130-1136, 2023.
Data files:
References
  1. [1] G. Păun, G. Rozenberg, and A. Salomaa (Eds.), “Handbook of Membrane Computing,” Oxford University Press, Cambridge, 2010.
  2. [2] G. Păun and R. Păun, “Membrane computing and economics: Numerical P systems,” Fundamenta Informaticae, Vol.73, Nos.1-2, pp. 213-227, 2006.
  3. [3] B. Aman and G. Ciobanu, “Behavioural Equivalences in Real-Time P Systems,” CMC2013, pp. 49-62, 2013. https://doi.org/10.1007/978-3-642-54239-8_8
  4. [4] H. Adorna, G. Păun, and M. Pérez-Jiménez, “On Communication Complexity in Evolution-Communication P systems,” Romanian J. of Information Science and Technology, Vol.13, No.2, pp. 113-130, 2010.
  5. [5] C. Dragomir, F. Ipate, S. Konur, R. Lefticaru, and L. Mierla, “Model Checking Kernel P Systems,” CMC2013, pp. 131-152, 2013. https://doi.org/10.1007/978-3-642-54239-8_12
  6. [6] B. Song, X. Zeng, and A. Rodríguez-Patón, “Monodirectional tissue P systems with channel states,” Information Sciences, Vol.546, pp. 206-219, 2021. https://doi.org/10.1016/j.ins.2020.08.030
  7. [7] X. Song, L. Valencia-Cabrera, H. Peng, and J. Wang, “Spiking neural P systems with autapses,” Information Sciences, Vol.570, pp. 383-402, 2021.
  8. [8] T. Wu, L. Zhang, and L. Pan, “Spiking neural P systems with target indications,” Theoretical Computer Science, Vol.862, pp. 250-261, 2021. https://doi.org/10.1016/j.tcs.2020.07.016
  9. [9] R. Freund, Y. Rogozhin, and S. Verlan, “Computational Completeness with Generating and Accepting P Systems Using Minimal Left and Right Insertion and Deletion,” CMC2013, pp. 321-324, 2013.
  10. [10] A. Leporati, “Computational Complexity of P Systems with Active Membranes,” CMC2013, pp. 19-32, 2013. https://doi.org/10.1007/978-3-642-54239-8_3
  11. [11] C. Martín-Vide, G. Păun, J. Pazos, and A. Rodríguez-Patón, “Tissue P systems,” Theoretical Computer Science, Vol.296, No.2, pp. 295-326, 2003. https://doi.org/10.1016/S0304-3975(02)00659-X
  12. [12] M. Ionescu, G. Păun, and T. Yokomori, “Spiking Neural P Systems,” Fundamenta Informaticae, Vol.71, No.2, pp. 279-308, 2006.
  13. [13] L. Pan, X. Zeng, and X. Zhang, “Time-Free Spiking Neural P Systems,” Neural Computation, Vol.23, No.5, pp. 1320-1342, 2011. https://doi.org/10.1162/NECO_a_00115
  14. [14] J. Xue and X. Liu, “Lattice Based Communication P Systems with Applications in Cluster Analysis,” Soft Computing, Vol.18, pp. 1425-1440, 2014. https://doi.org/10.1007/s00500-013-1155-y
  15. [15] R. Freund and S. Verlan, “A Formal Framework for Static (Tissue) P Systems,” LNCS, Vol.4860, pp. 271-284, 2007. https://doi.org/10.1007/978-3-540-77312-2_17
  16. [16] S. Verlan, “Using the Formal Framework for P Systems,” CMC2013, pp. 37-38, 2013. https://doi.org/10.1007/978-3-642-54239-8_6
  17. [17] J. Wang, H. J. Hoogeboom, and L. Pan, “Spiking Neural P Systems with Neuron Division,” LNCS, Vol.6501, pp. 361-376, 2010. https://doi.org/10.1007/978-3-642-18123-8_28
  18. [18] M. A. Gutiérrez-Naranjo, M. J. Pérez-Jiménez, and F. J. Romero-Campero, “A uniform solution to SAT using membrane creation,” Theoretical Computer Science, Vol.371, Nos.1-2, pp. 54-61, 2007. https://doi.org/10.1016/j.tcs.2006.10.013
  19. [19] J. Pazos, A. Rodríguez-Patón, and A. Silva, “Solving SAT in Linear Time with a Neural-Like Membrane System,” LNCS, Vol.2686, pp. 662-669, 2003. https://doi.org/10.1007/3-540-44868-3_84
  20. [20] C. Martín-Vide, J. Pazosc, G. Păun, and A. Rodríguez-Patón, “A New Class of Symbolic Abstract Neural Nets: Tissue P Systems,” Lecture Notes in Computer Science, Vol.2387, pp. 290-299, 2002. https://doi.org/10.1007/3-540-45655-4_32
  21. [21] L. Pan and A. Alhazov, “Solving HPP and SAT by P systems with active membranes and separation rules,” Acta Informatica, Vol.43, pp. 131-145, 2006. https://doi.org/10.1007/s00236-006-0018-8

Creative Commons License  This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.

*This site is desgined based on HTML5 and CSS3 for modern browsers, e.g. Chrome, Firefox, Safari, Edge, Opera.

Last updated on Apr. 22, 2024