Research Paper:
New Spatial Value Estimation Method for Curved Characteristic Line
Tomomasa Ohkubo†
 and Ei-ichi Matsunaga
and Ei-ichi Matsunaga
Department of Mechanical Engineering, Tokyo University of Technology
1404-1 Katakura, Hachioji, Tokyo 192-0982, Japan
†Corresponding author
Numerical calculations are used in various situations. However, to achieve accurate numerical calculations, accuracy in the calculation method and initial values with high spatial resolution are necessary. Therefore, we propose a new method for estimating spatial values that considers characteristic theory but does not use interpolation. We consider the treatment of the curved characteristic line, which implies that the characteristic speed is altered locally. In the new method named averaging inverse characteristics method (AICM), the locally changing characteristic speed is averaged with the characteristic speed of the previous steps. We calculated the spatial values of the shock tube problem, described by the Euler equation, and examined the accuracy of the AICM by comparing the results of the inverse characteristics method (ICM) proposed in the previous study and the traditional interpolating methods. Compared to other methods, AICM reduced the error to less than 1/10 for all parameters. We determined from these results that the AICM accurately estimates the spatial distribution of problems where characteristic speed has significantly changed.
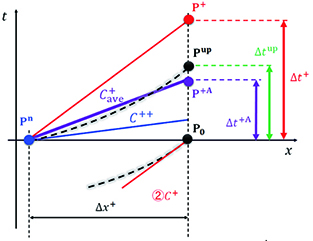
Concept of the new estimation method AICM
- [1] A. Arakawa, “Computational design for long-term numerical integration of the equations of fluid motion: Two-dimensional incompressible flow. Part I,” J. Comp. Phys., Vol.1, No.1, pp. 119-143, 1966. https://doi.org/10.1016/0021-9991(66)90015-5
- [2] S. A. Orszag, “Numerical simulation of incompressible flows within simple boundaries: Accuracy,” J. Fluid Mech., Vol.49, No.1, pp. 75-112, 1971. 10.1017/S0022112071001940
- [3] P. J. Sellers et al., “A simple biosphere model (SIB) for use within general circulation models,” J. Atmos. Sci., Vol.43, No.6, pp. 505-531, 1986. https://doi.org/10.1175/1520-0469(1986)043%3C0505:ASBMFU%3E2.0.CO;2
- [4] E. N. Lorenz, “The predictability of hydrodynamic flow,” Trans. N.Y. Acad. Sci. II, Vol.25, No.4, pp. 409-432, 1963.
- [5] P. Bauer, A. Thorpe, and G. Brunet, “The quiet revolution of numerical weather prediction,” Nature, Vol.525, No.7567, pp. 47-55, 2015. https://doi.org/10.1038/nature14956
- [6] W. Lahoz, B. Khattatov, and R. Menard (Eds.), “Data assimilation: Making sense of observations,” Springer, 2010. https://doi.org/10.1007/978-3-540-74703-1
- [7] M. Leutbecher and T. N. Palmer, “Ensemble forecasting,” J. Comput. Phys., Vol.227, No.7, pp. 3515-3539, 2008. https://doi.org/10.1016/j.jcp.2007.02.014
- [8] L. Espeholt et al., “Deep learning for twelve hour precipitation forecasts,” Nat. Commun., Vol.13, Article No.5145, 2022. https://doi.org/10.1038/s41467-022-32483-x
- [9] E. Matsunaga and T. Ohkubo, “Using the Characteristic Equation to Estimate the Initial Values for Numerical Forecasts,” J. Adv. Comput. Intell. Intell. Inform., Vol.20, No.7, pp. 1147-1151, 2016. https://doi.org/10.20965/jaciii.2016.p1147
- [10] K. Fukumitsu et al., “A new directional-splitting CIP interpolation with high accuracy and low memory consumption,” J. Comput. Phys., Vol.286, pp. 62-69, 2015. https://doi.org/10.1016/j.jcp.2014.12.045
- [11] T. Nakamura and D. Ajima, “A new interpolation method with high accuracy and low memory consumption for CIP-Soroban method,” Trans. Jpn. Soc. Comput. Eng. Sci., Vol.2016, Article No.20160014, 2016 (in Japanese). https://doi.org/10.11421/jsces.2016.20160014
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.