Paper:
Soft Sensor Model for Estimating the POI Displacement Based on a Dynamic Neural Network
Yujie Li*,**, Ming Zhang*,**,†, Yu Zhu*,**, Xin Li*,**, and Leijie Wang*,**
*State Key Lab of Tribology, Tsinghua University
Haidian District, Beijing 100084, China
**Beijing Key Lab of Precision/Ultra-Precision Manufacturing Equipments and Control, Tsinghua University
Haidian District, Beijing 100084, China
†Corresponding author
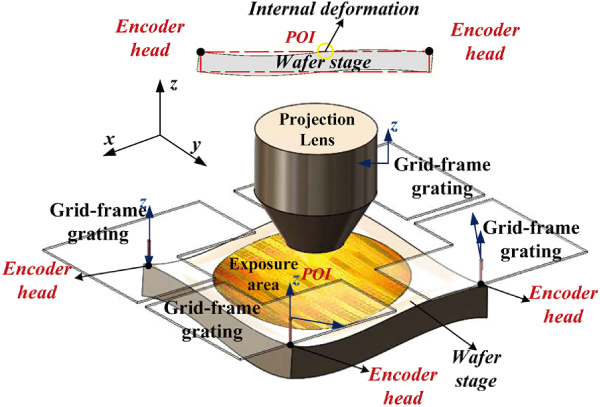
To satisfy the increasingly demanding requirements in throughput and accuracy, more lightweight structures and a higher control bandwidth are highly desirable in next-generation motion stages. However, these requirements lead to a more flexible deformation, causing the estimation accuracy of the point of interest (POI) displacement to be guaranteed under the rigid-body assumption. In this study, a soft sensor model is constructed using a dynamic neural network (DNN) to estimate the POI displacement. This model can reflect the dynamic characteristics of the POI and realize accurate estimations. Moreover, a method combining stepwise and weight methods is proposed to analyze the influence of different DNNs, and a performance measure is presented to evaluate the soft sensor model. In the simulation, the DNN with the hidden feedbacks is proved to be the most suitable soft sensor model. The relative error and correlation coefficient obtained were less than 2% and 0.9998, respectively, during training and 5% and 0.9989, respectively, during testing. Compared with the data-driven model using the least-squares method, the proposed method exhibits a higher precision, and the relative error is within the setting range using the proposed performance measure.
Deformation of the POIs
- [1] R.-H. M. Schmidt, “Ultra-precision engineering in lithographic exposure equipment for the semiconductor industry,” Philosophical Trans. of the Royal Society A: Mathematical, Physical and Engineering Sciences, Vol.370, No.1973, pp. 3950-3972, 2012.
- [2] T. Oomen et al., “Connecting system identification and robust control for next-generation motion control of a wafer stage,” IEEE Trans. on Control Systems Technology, Vol.22, No.1, pp. 102-118, 2014.
- [3] T. Oomen, E. Grassens, and F. Hendriks, “Inferential motion control: Identification and robust control framework for positioning an unmeasurable point of interest,” IEEE Trans. on Control Systems Technology, Vol.23, No.4, pp. 1602-1610, 2015.
- [4] T. Oomen, E. Grassens, F. Hendriks et al., “Inferential motion control: Identification and robust control with unmeasured performance variables,” 2011 50th IEEE Conf. on Decision and Control and European Control Conf., pp. 964-969, 2011.
- [5] M. Dorosti, R. Fey, M. Heertjes et al., “Finite element model reduction and model updating of structures for control,” IFAC Proc. Volumes, Vol.47, No.3, pp. 4517-4522, 2014.
- [6] G. Van Baars, “Getting high tech systems in shape and fit for the future,” Mikroniek, Vol.52, No.2, pp. 30-36, 2012.
- [7] H. Butler, “Position control in lithographic equipment,” IEEE Control Systems Magazine, Vol.31, No.5, pp. 28-47, 2011.
- [8] M. Dorosti, “Reduced-order model updating for prediction of performance variables in mechanical structures,” Eindhoven University of Technology, 2017.
- [9] H. Butler, “Acceleration feedback in a lithographic tool,” Control Engineering Practice, Vol.20, No.4, pp. 453-464, 2012.
- [10] R. A. C. M. Beerens, A. B. Jeunink, M. M. J. Van De Wal et al., “Positioning system, lithographic apparatus and device manufacturing method,” US Patent 9,383,659, 2016.
- [11] T. Castenmiller, F. van de Mast, T. de Kort et al., “Towards ultimate optical lithography with NXT: 1950i dual stage immersion platform,” Optical Microlithography XXIII, Int. Society for Optics and Photonics, pp. 7640:76401N, 2010.
- [12] M. Yasuda, S. Wakamoto, H. Imagawa et al., “Stability and calibration of overlay and focus control for a double patterning immersion scanner,” Optical Microlithography XXIV, Int. Society for Optics and Photonics, pp. 7973:79730Z, 2011.
- [13] C. Brosilow and B. Joseph, “Techniques of model-based control,” Prentice Hall, 2002.
- [14] F. A. A. Souza, R. Araújo, and J. Mendes, “Review of soft sensor methods for regression applications,” Chemometrics and Intelligent Laboratory Systems, Vol.152, pp. 69-79, 2016.
- [15] P. Kadlec, R. Grbić, and B. Gabrys, “Review of adaptation mechanisms for data-driven soft sensors,” Computers & Chemical Engineering, Vol.35, No.1, pp. 1-24, 2011.
- [16] H. Jin, X. Chen, J. Yang et al., “Online local learning based adaptive soft sensor and its application to an industrial fed-batch chlortetracycline fermentation process,” Chemometrics and Intelligent Laboratory Systems, Vol.143, pp. 58-78, 2015.
- [17] J. C. O’Callahan, “System equivalent reduction expansion process,” Proc. of the 7th Int. Modal Analysis Conf., pp. 29-37, 1989.
- [18] K. W. Verkerk, H. Butler, and P. P. J. van den Bosch, “Improved disturbance rejection for high precision systems through estimation of the flexible modes,” 2015 IEEE Conf. on Control Applications (CCA), pp. 1191-1196, 2015.
- [19] R. Voorhoeve, N. J. Dirkx, T. J. Melief et al., “Estimating structural deformations for inferential control: a disturbance observer approach,” IFAC-PapersOnLine, Vol.49, No.21, pp. 642-648, 2016.
- [20] A. H. Koevoets, J. van der Sanden, and T. Ruijl, “Thermal-elastic compensation models for position control,” Proc. of the 24th Annual Meeting of the American Society for Precision Engineering (ASPE), 2009.
- [21] J. G. Vogel, A. T. Ruiz, J. W. Spronck et al., “Estimation of the deformation of a plate using a limited number of sensors,” Proc. 2013 MIT & American Society for Precision Engineering Spring Topical Meeting on Precision Control for Advanced Manufacturing Systems, pp. 70-75, 2013.
- [22] G. P. Zhang, “Time series forecasting using a hybrid ARIMA and neural network model,” Neurocomputing, Vol.50, pp. 159-175, 2003.
- [23] N. I. Sapankevych and R. Sankar, “Time series prediction using support vector machines: a survey,” IEEE Computational Intelligence Magazine, Vol.4, No.2, pp. 24-38, 2009.
- [24] A. Prieto, B. Prieto, E. M. Ortigosa et al., “Neural networks: An overview of early research, current frameworks and new challenges,” Neurocomputing, Vol.214, pp. 242-268, 2016.
- [25] K. Benmahdjoub, Z. Ameur, and M. Boulifa, “Forecasting of rainfall using time delay neural network in Tizi-Ouzou (Algeria),” Energy Procedia, Vol.36, pp. 1138-1146, 2013.
- [26] A. Y. Hatata and M. Eladawy, “Prediction of the true harmonic current contribution of nonlinear loads using NARX neural network,” Alexandria Engineering J., Vol.57, No.3, pp. 1509-1518, 2018.
- [27] M. Ardalani-Farsa and S. Zolfaghari, “Chaotic time series prediction with residual analysis method using hybrid Elman–NARX neural networks,” Neurocomputing, Vol.73, No.13-15, pp. 2540-2553, 2010.
- [28] A. H. Jafari, R. Dhaouadi, and A. Jhemi, “Nonlinear Friction Estimation in Elastic Drive Systems Using a Dynamic Neural Network-Based Observer,” J. Adv. Comput. Intell. Intell. Inform., Vol.17, No.4, pp. 637-646, 2013.
- [29] S. Aras and İ. D. Kocakoç, “A new model selection strategy in time series forecasting with artificial neural networks: IHTS,” Neurocomputing, Vol.174, Part B, pp. 974-987, 2016.
- [30] G. Zhang, B. E. Patuwo, and M. Y. Hu, “Forecasting with artificial neural networks: The state of the art,” Int. J. of forecasting, Vol.14, No.1, pp. 35-62, 1998.
- [31] “Choose a Multi-layer Neural Network Training Function,” 2018, http://cn.mathworks.com/help/nnet/ug/choose-a-multilayer-neural-network-training-function.html [accessed October 29, 2021]
- [32] G. B. Ruben, K. Zhang, H. Bao et al., “Application and sensitivity analysis of artificial neural network for prediction of chemical oxygen demand,” Water Resources Management, Vol.32, No.1, pp. 273-283, 2018.
- [33] M. Gevrey, I. Dimopoulos, and S. Lek, “Review and comparison of methods to study the contribution of variables in artificial neural network models,” Ecological Modeling, Vol.160, No.3, pp. 249-264, 2003.
- [34] G. D. Garson, “Interpreting neural-network connection weights,” AI Expert, Vol.6, No.4, pp. 46-51, 1991.
- [35] P. Howes and N. Crook, “Using input parameter influences to support the decisions of feedforward neural networks,” Neurocomputing, Vol.24, No.1-3, pp. 191-206, 1999.
- [36] J. Sola and J. Sevilla, “Importance of input data normalization for the application of neural networks to complex industrial problems,” IEEE Trans. on Nuclear Science, Vol.44, No.3, pp. 1464-1468, 1997.
- [37] R. Boshuisen, “Analysis and performance of a lightweight over-actuated 450mm wafer chuck,” Eindhoven University of Technology, 2010.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.