Paper:
Self-Organized Subpopulation Based on Multiple Features in Genetic Programming on GPU
Keiko Ono* and Yoshiko Hanada**
*Doshisha University
1-3 Tatara Miyakodani, Kyotanabe, Kyoto 610-0394, Japan
**Kansai University
3-3-35 Yamate-cho, Suita, Osaka 564-8680, Japan
Genetic Programming (GP) is an Evolutionary Computation (EC) algorithm. Controlling genetic diversity in GP is a fundamental requirement to obtain various types of local minima effectively; however, this control is difficult compared to other EC algorithms because of difficulties in measuring the similarity between solutions. In general, common subtrees and the edit distance between solutions is used to evaluate the similarity between solutions. However, there are no clear guidelines regarding the best features to evaluate it. We hypothesized that the combination of multiple features helps to express the specific genetic similarity of each solution. In this study, we propose a self-organized subpopulation model based on similarity in terms of multiple features. To reconstruct subpopulations, we introduce a novel weighted network based on each normalized feature and utilize network clustering techniques. Although we can regard similarity as a correlation network between solutions, the use of multiple features incurs high computational costs, however, calculating the similarity is very suitable for parallelization on GPUs. Therefore, in the proposed method, we use CUDA to reconstruct subpopulations. Using three benchmark problems widely adopted in studies in the literature, we demonstrate that performance improvement can be achieved by reconstructing subpopulations based on a correlation network of solutions, and that the proposed method significantly outperforms typical methods.
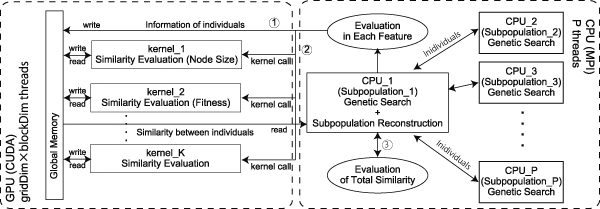
Proposed self-organized subpopulation based on multiple futures in genetic programming on GPU
- [1] K. A. De Jong, “An Analysis of the Behavior of a Class of Genetic Adaptive Systems,” Ph.D. thesis, University of Michigan, 1975.
- [2] B. L. Miller and M. J. Shaw, “Genetic Algorithms with Dynamic Niche Sharing for Multimodal Function Optimization,” Proc. of 1996 IEEE Int. Conf. on Evolutionary Computation (ICEC’96), pp. 786-791, 1996.
- [3] J. Hu, E. D. Goodman, and K. Seo, “Continuous Hierarchical Fair Competition Model for Sustainable Innovation in Genetic Programming,” R. Riolo and B. Worzel (Eds.), “Genetic Programming Theory and Practice,” pp. 81-98, Kluwer Academic Publishers, 2003.
- [4] J. Hu, E. D. Goodman, K. Seo, and M. Pei, “Adaptive Hierarchical Fair Competition (AHFC) Model for Parallel Evolutionary Algorithms,” Proc. of the Genetic and Evolutionary Computation Conf. 2002 (GECCO 2002), pp. 772-779, 2002.
- [5] G. S. Hornby, “ALPS: the age-layered population structure for reducing the problem of premature convergence,” Proc. of the 8th Annual Conf. on Genetic and Evolutionary Computation (GECCO’06), pp. 815-822, 2006.
- [6] G. S. Hornby, “Steady-state ALPS for real-valued problems,” Proc. of the 11th Annual Conf. on Genetic and Evolutionary Computation (GECCO’09), pp. 795-802, 2009.
- [7] J. M. Luna, J. R. Romero, C. Romero, and S. Ventura, “Discovering Subgroups by Means of Genetic Programming,” Proc. of the 16th European Conf. on Genetic Programming (EuroGP 2013), pp. 121-132, 2013.
- [8] Y. Jin, “Surrogate-assisted evolutionary computation: Recent advances and future challenges,” Swarm and Evolutionary Computation, Vol.1, Issue 2, pp. 61-70, 2011.
- [9] D. Andre and J. R. Koza, “A Parallel Implementation of Genetic Programming That Achieves Super-Linear Performance,” Proc. of the Int. Conf. on Parallel and Distributed Processing Techniques and Applications (PDPTA’96), Vol.III, pp. 1163-1174, 1996.
- [10] W. F. Punch, “How Effective Are Multiple Populations in Genetic Programming,” Genetic Programming 1998: Proc. of the 3rd Annual Conf., pp. 308-313, 1998.
- [11] M. Harwerth, “Experiments on Islands,” Proc. of the 14th European Conf. on Genetic Programming (EuroGP 2011), pp. 239-249, 2011.
- [12] S. Harding and W. Banzhaf, “Fast Genetic Programming and Artificial Developmental Systems on GPUs,” Proc. of the 21st Int. Symp. on High Performance Computing Systems and Applications (HPCS’07), doi: 10.1109/HPCS.2007.17, 2007.
- [13] S. Harding and W. Banzhaf, “Genetic programming on GPUs for image processing,” Int. J. of High Performance System Architecture, Vol.1, Issue 4, pp. 231-240, 2008.
- [14] I. Arnaldo, K. Veeramachaneni, and U.-M. O’Reilly, “Flash: A GP-GPU Ensemble Learning System for Handling Large Datasets,” Proc. of the 17th European Conf. on Genetic Programming (EuroGP 2014), pp. 13-24, 2014.
- [15] W. B. Langdon and M. Harman, “Genetically Improved CUDA C++ Software,” Proc. of the 17th European Conf. on Genetic Programming (EuroGP 2014), pp. 87-99, 2014.
- [16] W. B. Langdon, “A Many Threaded CUDA Interpreter for Genetic Programming,” Proc. of the 13th European Conf. on Genetic Programming (EuroGP 2010), pp. 146-158, 2010.
- [17] K. Ono and Y. Hanada, “A CUDA-based self-adaptive subpopulation model in genetic programming: CuSASGP,” Proc. of the 2015 IEEE Congress on Evolutionary Computation (CEC), pp. 1543-1550, 2015.
- [18] M. Girvan and M. E. J. Newman, “Community structure in social and biological networks,” Proc. of the National Academy of Science of the United States of America, Vol.99, No.12, pp. 7821-7826, 2002.
- [19] A. Clauset, M. E. J. Newman, and C. Moore, “Finding community structure in very large networks,” Physical Review E, Vol.70, Issue 6, doi: 10.1103/PhysRevE.70.066111, 2004.
- [20] K. Yanai and H. Iba, “Estimation of distribution programming based on Bayesian network,” Proc. of the 2003 Congress on Evolutionary Computation (CEC’03), Vol.3, pp. 1618-1625, 2003.
- [21] W. B. Langdon and R. Poli, ”Foundations of Genetic Programming,” Springer, 2002.
- [22] W. B. Langdon and R. Poli, “Why Ants are Hard,” Genetic Programming 1998: Proc. of the 3rd Annual Conf., pp. 193-201, 1998.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.