Paper:
Intelligent Compensating Method for MPC-Based Deviation Correction with Stratum Uncertainty in Vertical Drilling Process
Dian Zhang*,**,***, Min Wu*,**,***,†, Chengda Lu*,**,***, Luefeng Chen*,**,***, Weihua Cao*,**,***, and Jie Hu*,**,***
*School of Automation, China University of Geosciences
No.388 Lumo Road, Hongshan, Wuhan, Hubei 430074, China
**Hubei Key Laboratory of Advanced Control and Intelligent Automation for Complex Systems
No.388 Lumo Road, Hongshan, Wuhan, Hubei 430074, China
***Engineering Research Center of Intelligent Technology for Geo-Exploration, Ministry of Education
No.388 Lumo Road, Hongshan, Wuhan, Hubei 430074, China
†Corresponding author
With the rapid development of control technology, increasing applications are using model predictive control (MPC) for deviation correction in vertical drilling. However, the accuracy of the predictive model is affected by the uncertainty of the stratum, which results in model mismatch and a reduction in control performance. In this paper, an intelligent compensating method is proposed for MPC-based deviation correction with stratum uncertainty in a vertical drilling process to increase control accuracy. First, a trajectory extension model is introduced as the predictive model for MPC, and the uncertainty of the stratum is discussed. Then, the compensation for the MPC is acquired based on a Gaussian fitting method and hybrid bat algorithm. Finally, based on the actual drilling data, a simulation is performed to demonstrate the effectiveness of the proposed method.
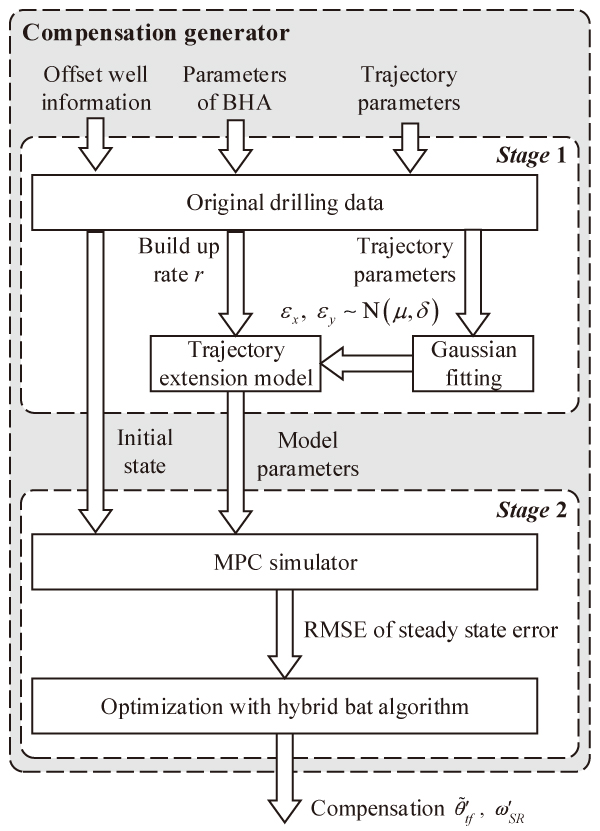
Flowchart of the compensation method
- [1] W. Wang, H. Zhang, N. Li, C. Wang, X. Teng, W. Zhu, and Q. Di, “The dynamic deviation control mechanism of the prebent pendulum BHA in air drilling,” J. of Petroleum Science and Engineering, Vol.176, pp. 521-531, 2019.
- [2] W. Huang, D. Gao, and Y. Liu, “Buckling analysis of tubular strings with connectors constrained in vertical and inclined wellbores,” SPE J., Vol.23, No.2, pp. 301-327, 2018.
- [3] Y. D. Lu, L. C. Zeng, F. L. Zeng, and G. S. Kai, “Dynamic simulation and research on hydraulic guide system of automatic vertical drilling tool,” Materials Research Innovations, Vol.19, No.s6, pp. 170-174, 2015.
- [4] N. Panchal, M. T. Bayliss, and J. F. Whidborne, “Attitude control system for directional drilling bottom hole assemblies,” IET Control Theory & Applications, Vol.6, No.7, pp. 884-892, 2012.
- [5] N. A. H. Kremers, E. Detournay, and N. van de Wouw, “Model-based robust control of directional drilling systems,” IEEE Trans. on Control Systems Technology, Vol.24, No.1, pp. 226-239, 2016.
- [6] Z. Cai, X. Z. Lai, M. Wu, L. F. Chen, and C. D. Lu, “Compensation control for tool attitude in directional drilling systems,” Proc. of the 12th Asian Control Conf. (ASCC 2019), pp. 376-380, 2019.
- [7] M. Bayliss, C. Bogath, and J. Whidborne, “MPC-based feedback delay compensation scheme for directional drilling attitude control,” SPE/IADC Drilling Conf. and Exhibition, 2015.
- [8] N. Demirer, U. Zalluhoglu, J. Marck, R. Darbe, and M. Morari, “Autonomous directional drilling with rotary steerable systems,” 2019 American Control Conf. (ACC), pp. 5203-5208, 2019.
- [9] D. Zhang, M. Wu, L. F. Chen, C. D. Lu, and W. H. Cao, “Model predictive control strategy based on improved trajectory extension model for deviation correction in vertical drilling process,” 21st IFAC World Congress, 2020.
- [10] M. Farina, L. Giulioni, L. Magni, and R. Scattolini, “An approach to output-feedback MPC of stochastic linear discrete-time systems,” Automatica, Vol.55, pp. 140-149, 2015.
- [11] X. Tang, L. Deng, N. Liu, S. Yang, and J. Yu, “Observer-based output feedback MPC for T–S fuzzy system with data loss and bounded disturbance,” IEEE Trans. on Cybernetics, Vol.49, No.6, pp. 2119-2132, 2018.
- [12] J. Hu and B. Ding, “A periodic approach to dynamic output feedback MPC for quasi-LPV model,” IEEE Trans. on Automatic Control, doi: 10.1109/TAC.2020.3002162, 2020.
- [13] B. Das and P. Mhaskar, “Adaptive output-feedback Lyapunov-based model predictive control of nonlinear process systems,” Int. J. of Robust and Nonlinear Control, Vol.28, No.5, pp. 1597-1609, 2018.
- [14] F. A. Hasan, A. T. Humod, and L. J. Rashad, “Robust decoupled controller of induction motor by combining PSO and Kharitonov’s theorem,” Engineering Science and Technology, an Int. J., Vol.23, No.6, pp. 1415-1424, doi: 10.1016/j.jestch.2020.04.004, 2020.
- [15] D. Pal, A. Chatterjee, and A. Rakshit, “Robust-stable quadratic-optimal fuzzy-PDC controllers for systems with parametric uncertainties: A PSO based approach,” Engineering Applications of Artificial Intelligence, Vol.70, pp. 38-51, 2018.
- [16] H. Feng, C.-B. Yin, W.-W. Weng, W. Ma, J.-J. Zhou, W.-H. Jia, and Z.-L. Zhang, “Robotic excavator trajectory control using an improved GA based PID controller,” Mechanical Systems and Signal Processing, Vol.105, pp. 153-168, 2018.
- [17] W. M. Elawady, S. M. Lebda, and A. M. Sarhan, “An optimized fuzzy continuous sliding mode controller combined with an adaptive proportional-integral-derivative control for uncertain systems,” Optimal Control Applications and Methods, Vol.41, No.3, pp. 980-1000, 2020.
- [18] E. V. Kumar, G. S. Raaja, and J. Jerome, “Adaptive PSO for optimal LQR tracking control of 2 DoF laboratory helicopter,” Applied Soft Computing, Vol.41, pp. 77-90, 2016.
- [19] E.-C. Chang, Z. Su, Z. Xu, and R.-C. Wu, “Particle swarm optimization tuned fuzzy terminal sliding mode control for UPS inverters,” J. of Intelligent & Fuzzy Systems, Vol.29, No.6, pp. 2483-2488, 2015.
- [20] M. Navabi, H. Mirzaei, and A. Davoodi, “Optimum design of robust adaptive controller with actuator constraints,” Int. J. of Control, Automation and Systems, Vol.18, No.11, pp. 2734-2741, doi: 10.1007/s12555-019-0356-2, 2020.
- [21] C.-H. Cheng, P.-J. Cheng, and M.-J. Xie, “Current sharing of paralleled DC–DC converters using GA-based PID controllers,” Expert Systems with Applications, Vol.37, No.1, pp. 733-740, 2010.
- [22] C. Gan, W.-H. Cao, K.-Z. Liu, M. Wu, F.-W. Wang, and S.-B. Zhang, “A new hybrid bat algorithm and its application to the ROP optimization in drilling processes,” IEEE Trans. on Industrial Informatics, Vol.16, No.12, pp. 7338-7348, doi: 10.1109/TII.2019.2943165, 2020.
- [23] A. Wilson, “Bending rules with high-build-rate rotary-steerable systems,” J. of Petroleum Technology, Vol.68, No.12, pp. 62-63, 2016.
- [24] Production Department, American Petroleum Institute, “Bulletin on directional drilling survey calculation methods and terminology,” American Petroleum Institute, pp. 1862-1867, 1985.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.