Paper:
Optimization Design of Oven Shape Based on Heat Distribution Model
Xueyong Yu, Weiran Lin†, Jinling Wei, Shuoping Wang, and Haifeng Ke
School of Computer and Computing Science, Zhejiang University City College
No.51 Huzhou Street, Gongshu District, Hangzhou, Zhejiang 310015, China
†Corresponding author
We developed two models in this study: one to show the distribution of heat for pans of different shapes, and the other to select the best type of pan to maximize the number of pans that can fit in the oven and to maximize even heat distribution in the pans. We constructed a model of heat distribution. The uneven distribution of heat is mainly caused by heat conduction. We established a differential equation for heat conduction according to Fourier’s law. The finite-difference method and Gauss-Seidel iteration were used to solve the equation, and MATLAB was used to draw the corresponding heat-distribution chart. We built a quantitative model of the shape optimization with an evaluation equation. Using the permutation and combination method, we calculated the maximum number of pans and the utilization rate of area. Finally, we determined that the optimal pan type is a round square, which achieved the best state.
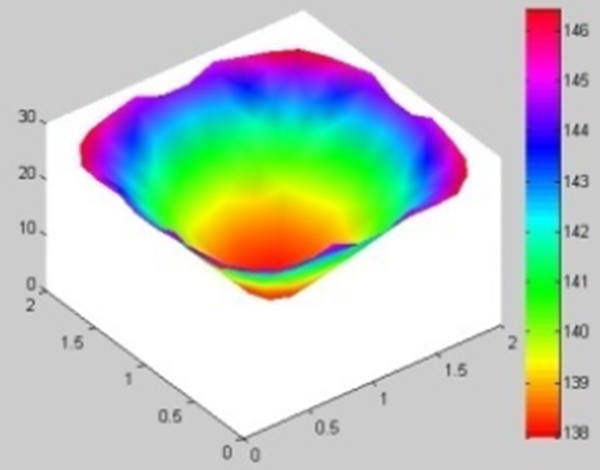
Heat distribution in oven
- [1] M. Chu, “Recipe File: Dark Chocolate Brownies,” http://www.cookingforengineers.com/recipe/158/Dark-Chocolate-Brownies [accessed March 29, 2019]
- [2] X.-Q. Wang and X.-B. Ma, “A Exploration of the Food Heated in the Household Microwave Oven and Leaves,” The Food Industry, Vol.2013, No.11, pp. 195-198, 2013 (in Chinese).
- [3] Q. Zhu and X. Chen, “Application of PDE Toolbox and Least Square Method in Heat Conduction of Metal,” Process Automation Instrumentation, Vol.32, No.6, pp. 26-28+31, 2011 (in Chinese).
- [4] Y.-F. Li et al., “Analysis and Structural Improvement of Flow Field of Heat-shrinkable Oven,” Packaging Engineering, Vol.38, No.3, pp. 83-88, 2017 (in Chinese).
- [5] L. David, B. Nacer, B. Pascal, and J. Gérard, “Transient radiative and conductive heat transfer in non-gray semitransparent two-dimensional media with mixed boundary conditions,” Heat and Mass Transfer, Vol.42, No.4, pp. 322-337, 2006.
- [6] Q. Xue and X. Xiao, “Two dimensional heat conduction equation finite volume method to achieve on MATLAB,” Computer Engineering and Applications, Vol.48, No.24, pp. 197-200+221, 2012 (in Chinese).
- [7] T. Flatberg et al., “Temperature distribution in an oven for calibrating thermometers,” Proc. of the 9th ECMI Modelling Week, pp. 183-199, 1997.
- [8] F. P. Incropera, D. P. Dewitt, T. L. Bergman, and A. S. Lavine, “Fundamentals of Heat and Mass Transfer,” 6th Edition, John Wiley & Sons, 2007.
- [9] Y. Zhang and E. Guo, “Heat Transfer,” Southeast University Press, 2004 (in Chinese).
- [10] Z.-B. Xu and J.-Q. Min, “The Numerical Simulation of Heat Conduction based on pdetool,” J. of Jiamusi University (Natural Science Edition), Vol.2006, No.2, pp. 270-272, 2006 (in Chinese).
- [11] J. Xiong and Z. Wei, “Applications of PDE-tool of MATLAB to Heat Conduction,” Industrial Heating, Vol.38, No.4, pp. 42-44, 2009 (in Chinese).
- [12] X. Shen, “Oven Fluid Analysis and Structure Optimization for Gravure Printing Machine YF93,” Master thesis, Xi’an University of Technology, 2013.
- [13] F. Asllanaj, G. Parent, and G. Jeandel, “Transient Radiation and Conduction Heat Transfer in a Gray Absorbing-Emitting Medium Applied on Two-Dimensional Complex-Shaped Domains,” Numerical Heat Transfer, Part B: Fundamentals, Vol.52, Issue 2, pp. 179-200, 2007.
- [14] Y. Song, K. Xu, and F. Yi, “The Design of Ultimate Brownie Pan,” Mathematical Modeling and Its Applications, Vol.2, No.2, pp. 62-71, 2013 (in Chinese).
- [15] L. Zhang, J. Bi, and L. Guo, “The Practical Textbook of MATLAB,” Posts & Telecom Press Co., Ltd., 2008 (in Chinese).
- [16] C. Shi, “Heat Conduction Equation Finite Difference Method to Achieve the MATLAB,” J. of Xianyang Normal University, Vol.24, No.4, pp. 27-29+36, 2009 (in Chinese).
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.