Paper:
Predictability of China’s Stock Market Returns Based on Combination of Distribution Forecasting Models
Yanyun Yao*, Xiutian Zheng**,†, and Huimin Wang*
*Department of Applied Statistics, Shaoxing University
900 Chengnan Avenue, Yuecheng District, Shaoxing, Zhejiang 312000, China
**Department of Economics, Hangzhou Normal University Qianjiang College
16 Xuelin Street, Xiasha University Town, Hangzhou, Zhejiang 310018, China
†Corresponding author
No consensus exists in the literature on whether stock prices can be predicted, with most existing studies employing point forecasting to predict returns. By contrast, this study adopts the new perspective of distribution forecasting to investigate the predictability of the stock market using the model combination strategy. Specifically, the Shanghai Composite Index and the Shenzhen Component Index are selected as research objects. Seven models – GARCH-norm, GARCH-sstd, EGARCH-sstd, EGARCH-sstd-M, one-component Beta-t-EGARCH, two-component Beta-t-EGARCH, and the EWMA-based nonparametric model – are employed to perform distribution forecasting of the returns. The results of out-of-sample forecasting evaluation show that none of the individual models is “qualified” in terms of predictive power. Therefore, three combinations of individual models were constructed: equal weight combination, log-likelihood score combination, and continuous ranked probability score combination. The latter two combinations were found to always have significant directional predictability and excess profitability, which indicates that the two combined models may be closer to the real data generation process; from the perspective of economic evaluation, they may have a predictive effect on the conditional return distribution in China’s stock market.
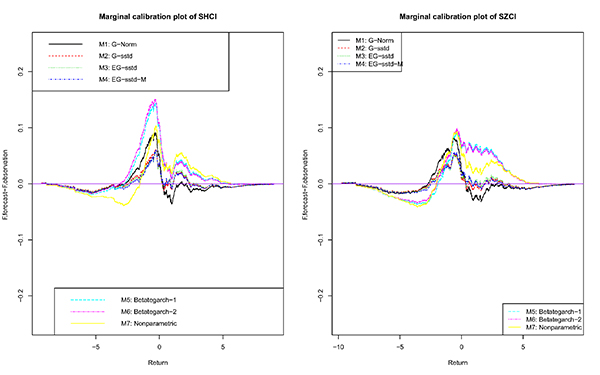
Marginal calibration charts of SHCI and SZCI
- [1] E. F. Fama, “Random walks in stock market prices,” Financial Analysts J., No.21, pp. 55-59, 1965.
- [2] A. W. Lo, “The adaptive markets hypothesis,” The J. of Portfolio Management, No.5, pp. 15-29, 2004.
- [3] E. F. Fama, “Efficient Capital Markets: II,” The J. of Finance, Vol.46, No.5, pp. 1575-1617, 1991.
- [4] J. H. Cochrane, “New facts in finance,” Economic Perspectives, Vol.23, No.3, pp. 36-58, 1999.
- [5] K. P. Lim, W. Luo, and J. H. Kim, “Are US stock index returns predictable? evidence from automatic autocorrelation-based tests,” Applied Economics, Vol.45, No.8, pp. 953-962, 2013.
- [6] X. Zhou, Q. Song, and X. Liu, “Adaptive markets hypothesis and evidence from China’s capital markets,” J. of Management Science, No.6, pp. 111-126, 2017 (in Chinese).
- [7] J. H. Cochrane, “The dog that did not bark: a defense of return predictability,” Review of Financial Studies, Vol.21, No.4, pp. 1533-1575, 2008.
- [8] W. E. Ferson, S. Sarkissian, and T. Simin, “Asset pricing models with conditional betas and alphas: the effects of data snooping and spurious regression,” J. of Financial and Quantitative Analysis, Vol.43, No.2, pp. 331-353, 2008.
- [9] J. T. Campbell and P. Samuel, “Predicting excess stock returns out of sample: can anything beat the historical average?,” Scholarly Articles, Vol.21, No.4, pp. 1509-1531, 2008.
- [10] Y. Zhang, Q. Zeng, F. Ma, and B. Shi, “Forecasting stock returns: do less powerful predictors help?,” Econ. Modell., doi: 10.1016/j.econmod.2018.09.014, 2018.
- [11] T. Dangl and M. Halling, “Predictive regressions with time-varying coefficients,” J. Financ. Econ., Vol.106, No.1, pp. 157-181, 2012.
- [12] X. Zhu and J. Zhu, “Predicting stock returns: a regime-switching combination approach and economic links,” J. Bank. Finance, Vol.37, No.11, pp. 4120-4133, 2013.
- [13] D. E. Rapach, J. K. Strauss, and G. Zhou, “Out-of-sample equity premium prediction: combination forecasts and links to the real economy,” Rev. Financ. Stud., Vol.23, No.2, pp. 821-862, 2010.
- [14] D. Massacci, “Predicting the distribution of stock returns: model formulation, statistical evaluation, VaR analysis and economic significance,” J. of Forecasting, No.34, pp. 191-208, 2015.
- [15] J. Zheng, H. Pan, and Y. Fan, “Analysis of return directional predictability of Chinese stock market based on generalized cross-spectrum approach,” China Soft Science, No.8, pp. 154-160, 2010 (in Chinese).
- [16] P. F. Christoffersen and F. X. Diebold, “Financial Asset Returns, Direction-of-Change Forecasting, and Volatility Dynamics,” Management Science, Vol,52, pp. 1273-1287, 2006.
- [17] L. Li, S. Guan, and M. Guan, “Economic analysis of time-varying distribution of stock market returns and empirical evidence in China,” Statistical Research, No.11, pp. 66-78, 2011 (in Chinese).
- [18] Y. Yao and B. Xu, “Conditional distribution prediction of stock returns and its application on risk aversion analysis,” J. Adv. Comput. Intell. Intell. Inform., Vol. 22, No.4, pp. 448-456, 2018.
- [19] L. Liu, R. Bu, Z. Pan, and Y. Xu, “Are financial returns really predictable out-of-sample? Evidence from a new bootstrap test,” Economic Modelling, Vol.81, pp. 124-135, 2019.
- [20] M. H. Pesaran and A. Timmermann, “A simple nonparametric test of predictive performance,” J. of Business and Economic Statistics, Vol.10, No.4, pp. 461-465, 1992.
- [21] S. Anatolyev and A. Gerko, “A trading approach to testing for predictability,” J. of Business and Economic Statistics, Vol.23, No.4, pp. 455-461, 2005.
- [22] M. H. Pesaran and A. Timmermann, “Real-time econometrics,” Econometric Theory, Vol.21, No.1, pp. 212-231, 2005.
- [23] R. F. Engle, “Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation,” Econometrica, Vol.50, No.4, pp. 987-1007, 1982.
- [24] T. Bollerslev, “Generalized autoregressive conditional heteroskedasticity,” J. of Econometrics, No.31, pp. 307-327, 1986.
- [25] P. Wang and J. Wang, “The return distribution of China’s stock market and its SPA test,” J. of Systems Management, Vol.17, No.5, pp. 542-547, 2008 (in Chinese).
- [26] D. B. Nelson, “Conditional heteroskedasticity in asset returns: A new approach,” Econometrica, Vol.59, No.2, pp. 347-370, 1991.
- [27] R. F. Engle, D. M. Lilien, and R. P. Robins, “Estimating time varying risk premia in the term structure: The arch-m model,” Econometrica: J. of the Econometric Society, Vol.55, No.2, pp. 391-407, 1987.
- [28] A. C. Harvey and T. Chakravarty, “Beta-t-(E)GARCH,” Cambridge Working Papers in Economics 0840, Faculty of Economics, University of Cambridge, 2008.
- [29] A. C. Harvey, “Dynamic models for volatility and heavy tails,” Cambridge University Press, 2013.
- [30] A. C. Harvey and G. Sucarrat, “EGARCH models with fat tails, skewness and leverage,” Computational Statistics and Data Analysis, No.76, pp. 320-338, 2014.
- [31] S. Blazsek and M. Villatoro, “Is Beta-t-EGARCH(1,1) superior to GARCH(1,1),” Applied Economics, Vol.47, No.17, pp. 1764-1774, 2015.
- [32] S. Blazsek and V. Mendoza, “QARMA-Beta-t-EGARCH versus ARMA-GARCH: an application to S&P 500,” Applied Economics, Vol.48, No.12, pp. 1119-1129, 2016.
- [33] Z. Ding, R. Engle, and C. Granger, “A long memory property of stock market returns and a new model,” J. of Empirical Finance, No.1, pp. 83-106, 1993.
- [34] A. Harvey and V. Oryshchenko, “Kernel density estimation for time series data,” Int. J. of Forecasting, No.28, pp. 3-14, 2012.
- [35] G. Elliott and A. Timmermann, “Economic forecasting,” Princeton University Press, 2016.
- [36] A. Pérez, “Comments on “Kernel density estimation for time series data”,” Int. J. of Forecasting, No.28, pp. 15-19, 2012.
- [37] J. Nowotarski and R. Weron, “Recent advances in electricity price forecasting: A review of probabilistic forecasting,” Renewable and Sustainable Energy Reviews, No.81, pp. 1548-1568, 2018.
- [38] A. P. Dawid, “Statistical theory: the prequential approach,” J R Stat Soc A, Vol.147, No.2, pp. 278-292, 1984.
- [39] F. X. Diebold, A. G. Todd, and S. T. Anthony, “Evaluating density forecasts with applications to financial risk management,” Int. Economic Review, Vol.39, No.4, pp. 863-883, 1998.
- [40] J. Berkowitz, “Testing density forecasts, with applications to risk management,” J. of Business and Economic Statistics, Vol.19, No.4, pp. 465-474, 2001.
- [41] A. Ghalanos, “Introduction to the rugarch package (Version 1.3-8),” 2020, https://cran.r-project.org/web/packages/rugarch/vignettes/Introduction_to_the_rugarch_package.pdf [accessed February 7, 2020]
- [42] Y. Hong and H. Li, “Nonparametric specification testing for continuous-time models with applications to term structure of interest rates,” Review of Financial Studies, Vol.18, No.1, pp. 37-84, 2005.
- [43] Y. Ait-Sahalia, “Testing continuous-time models of the spot interest rate,” Review of Financial Studies, Vol.9, No.2, pp. 385-426, 1996.
- [44] T. Gneiting, F. Balabdaoui, and A. E. Raftery, “Probabilistic forecasts, calibration and sharpness,” J. R. Statist. Soc. B, No.69, pp. 243-268, 2007.
- [45] A. Timmermann, “Forecast combinations,” G. Elliott, C. W. J. Granger, and A. Timmermann (Eds.), “Handbook of Economic Forecasting,” Volume 1, pp. 135-196, Elsevier, 2006.
- [46] S. G. Hall and J. Mitchell, “Combining density forecasts,” Int. J. of Forecasting, Vol.23, No.1, pp. 1-13, 2007.
- [47] M. Billio, R. Casarin, F. Ravazzolo, and K. D. Herman, “Time-varying combinations of predictive densities using nonlinear filtering,” J. of Econometrics, Vol.177, Issue 2, pp. 213-232, 2013.
- [48] M. H. Pesaran, C. Schleicher, and P. Zaffaroni, “Model averaging in risk management with an application to futures markets,” J. of Empirical Finance, Vol.16, No.2, pp. 280-305, 2009.
- [49] G. Leicht and J. E. Tanner, “Economic forecast evaluation: profits versus the conventional error measures,” American Economic Review, Vol.81, No.3, pp. 580-590, 1991.
- [50] J. Fan and Q. Yao, “Nonlinear time series: modeling, forecasting and application,” Higher Education Press, 2005 (in Chinese).
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.