Paper:
Forecasting Stock Index Futures Intraday Returns: Functional Time Series Model
Yizheng Fu, Zhifang Su†, Boyu Xu, and Yu Zhou
School of Economics and Finance, Huaqiao University
No.269 Chenghua North Road, Fengze District, Quanzhou, Fujian 362021, China
†Corresponding author
It is of great significance to forecast the intraday returns of stock index futures. As the data sampling frequency increases, the functional characteristics of data become more obvious. Based on the functional principal component analysis, the functional principal component score was predicted by BM, OLS, RR, PLS, and other methods, and the dynamic forecasting curve was reconstructed by the predicted value. The traditional forecasting methods mainly focus on “point” prediction, while the functional time series forecasting method can avoid the point forecasting limitation, and realize “line” prediction and dynamic forecasting, which is superior to the traditional analysis method. In this paper, the empirical analysis uses the 5-minute closing price data of the stock index futures contract (IF1812). The results show that the BM prediction method performed the best. In this paper, data are considered as a functional time series analysis object, and the interference caused by overnight information is removed so that it can better explore the intraday volatility law, which is conducive to further understanding of market microstructure.
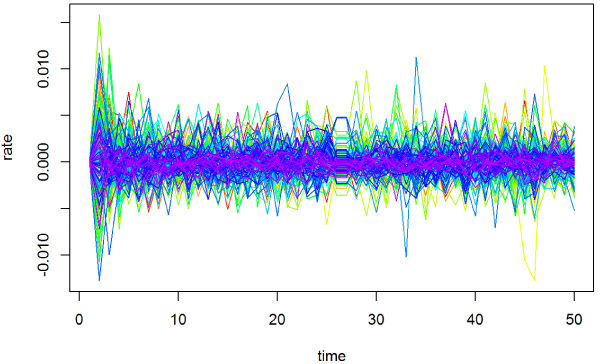
Intraday return (functional time series)
- [1] L. Zhou, “The influence of investor sentiment on commodity futures price and volatility – a case study of rebar futures,” Wuhan Finance, Vol.2019, No.6, pp. 27-32, 2019 (in Chinese).
- [2] S. Nie and M. Li, “Causal Analysis of Overnight and Lunch break Information for Chinese Stock Indexes and Futures,” J. of Applied Statistics and Management, Vol.38, No.4, pp. 719-731, 2019 (in Chinese).
- [3] J. Lin and Z. Gong, “A Research on Forecasting of Shanghai Zinc Futures Price Based on Artificial Neural Network,” The Theory and Practice of Finance and Economics, Vol.38, No.2, pp. 54-57, 2017 (in Chinese).
- [4] S. Wang, J. Wang, and G. Li, “Research and Prediction of High Frequency Intraday Yield of the CSI 300 Index Futures Based on ARMA Model,” J. of North China Electric Power University (Social Sciences), Vol.2018, No.3, pp. 71-79, 2018 (in Chinese).
- [5] J. Ramsay, “When the data are functions,” Psychometrika, Vol.47, Issue 4, pp. 379-396, 1982.
- [6] H. L. Shang, “Forecasting intraday S&P 500 index returns: A functional time series approach,” J. of Forecasting, Vol.36, No.7, pp. 741-755, 2017.
- [7] D. Bosq, “Nonparametric estimation and prediction for continuous time processes,” Nonlinear Analysis: Theory, Methods & Applications, Vol.30, Issue 6, pp. 3547-3551, 1997.
- [8] J. Klepsch and C. Klüppelberg, “An innovations algorithm for the prediction of functional linear processes,” J. of Multivariate Analysis, Vol.155, pp. 252-271, 2017.
- [9] J. Klepsch, C. Klüppelberg, and T. Wei, “Prediction of functional ARMA processes with an application to traffic data,” Econometrics and Statistics, Vol.1, pp. 128-149, 2017.
- [10] H. L. Shang, “Bootstrap methods for stationary functional time series,” Statistics and Computing, Vol.28, Issue 1, pp. 1-10, 2018.
- [11] R. J. Hyndman and H. L. Shang, “Forecasting functional time series,” J. of the Korean Statistical Society, Vol.38, Issue 3, pp. 199-211, 2009.
- [12] A. Aue, D. D. Norinho, and S. Hörmann, “On the Prediction of Stationary Functional Time Series,” J. of the American Statistical Association, Vol.110, Issue 509, pp. 378-392, 2015.
- [13] H. Shen, “On Modeling and Forecasting Time Series of Smooth Curves,” Technometrics, Vol.51, Issue 3, pp. 227-238, 2009.
- [14] H. L. Shang and R. J. Hyndman, “Nonparametric time series forecasting with dynamic updating,” Mathematics and Computers in Simulation, Vol.81, Issue 7, pp. 1310-1324, 2011.
- [15] S. Hays, H. Shen, and J. Z. Huang, “Functional Dynamic Factor Models with Application to Yield Curve Forecasting,” The Annals of Applied Statistics, Vol.6, No.3, pp. 870-894, 2012.
- [16] D. R. Kowal, D. S. Matteson, and D. Ruppert, “A Bayesian Multivariate Functional Dynamic Linear Model,” J. of the American Statistical Association, Vol.112, Issue 518, pp. 733-744, 2017.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.