Paper:
Recurrent Neural Network for Predicting Dielectric Mirror Reflectivity
Tomomasa Ohkubo*,†, Ei-ichi Matsunaga*, Junji Kawanaka**, Takahisa Jitsuno**, Shinji Motokoshi***, and Kunio Yoshida**
*Tokyo University of Technology
1404-1 Katakuramachi, Hachioji, Tokyo 192-0982, Japan
**Institute of Laser Engineering, Osaka University
2-6 Yamadaoka, Suita, Osaka 565-0871, Japan
***Institute for Laser Technology
1-8-4 Utsubo-honmachi, Nishi-ku, Osaka 550-0004, Japan
†Corresponding author
Optical devices often achieve their maximum effectiveness by using dielectric mirrors; however, their design techniques depend on expert knowledge in specifying the mirror properties. This expertise can also be achieved by machine learning, although it is not clear what kind of neural network would be effective for learning about dielectric mirrors. In this paper, we clarify that the recurrent neural network (RNN) is an effective approach to machine-learning for dielectric mirror properties. The relation between the thickness distribution of the mirror’s multiple film layers and the average reflectivity in the target wavelength region is used as the indicator in this study. Reflection from the dielectric multilayer film results from the sequence of interfering reflections from the boundaries between film layers. Therefore, the RNN, which is usually used for sequential data, is effective to learn the relationship between average reflectivity and the thickness of individual film layers in a dielectric mirror. We found that a RNN can predict its average reflectivity with a mean squared error (MSE) less than 10-4 from representative thickness distribution data (10 layers with alternating refractive indexes 2.3 and 1.4). Furthermore, we clarified that training data sets generated randomly lead to over-learning. It is necessary to generate training data sets from larger data sets so that the histogram of reflectivity becomes a flat distribution. In the future, we plan to apply this knowledge to design dielectric mirrors using neural network approaches such as generative adversarial networks, which do not require the know-how of experts.
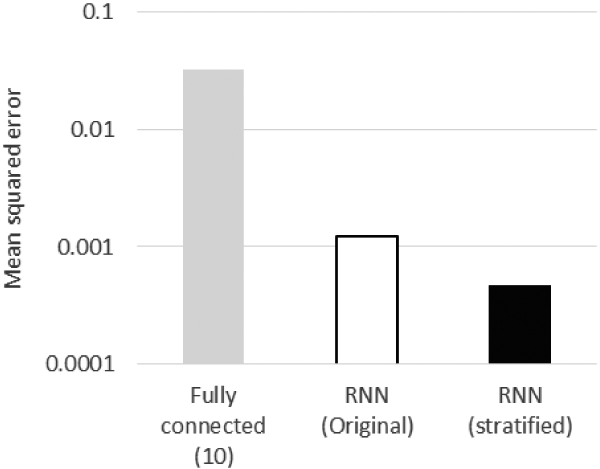
Comparison of MSE between results
- [1] P. Baumeister, “Design of Multilayer Filters by Successive Approximations,” J. of the Optical Society of America, Vol.48, Issue 12, pp. 955-958, 1958.
- [2] R. Szipőcs and A. Kőházi-Kis, “Theory and design of chirped dielectric laser mirrors,” Applied Physics B, Vol.65, Issue 2, pp. 115-135, 1997.
- [3] Y. Fujimoto et al., “Development on ultra-broadband high intense laser propagation optics for exa-watt laser,” ICUIL, 2012.
- [4] Y. Gal and Z. Ghahramani, “A theoretically grounded application of dropout in recurrent neural networks,” Proc. of the 30th Int. Conf. on Neural Information Processing Systems (NIPS’16), pp. 1027-1035, 2016.
- [5] S. Holmes and P. Kraatz, “Investigation of Pulsed CO Laser Damage in Coated Metal Mirrors and Dielectric-Coated Windows,” A. J. Glass and A. H. Guenter (Eds.), “Laser Induced Damage in Optical Materials: 1973,” pp. 138-150, U.S. Department of Commerce and National Bureau of Standards, 1973.
- [6] S. D. Smith, “Design of Multilayer Filters by Considering Two Effective Interfaces,” J. of the Optical Society of America, Vol.48, Issue 1, pp. 43-50, 1958.
- [7] M. Abadi et al., “TensorFlow: A system for large-scale machine learning,” TensorFlow White Papers, 2015.
- [8] F. Chollet et al., “Keras,” 2015, http://keras.io [accessed February 18, 2019]
- [9] R. H. R. Hahnloser, R. Sarpeshkar, M. A. Mahowald, R. J. Douglas, and H. S. Seung, “Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit,” Nature, Vol.405, pp. 947-951, 2000.
- [10] D. P. Kingma and J. Ba, “Adam: A Method for Stochastic Optimization,” Proc. of the 3rd Int. Conf. for Learning Representations, 2015.
- [11] Y. Wu, M. Schuster, Z. Chen, Q. V. Le, M. Norouzi, W. Macherey, M. Krikun, Y. Cao, Q. Gao, K. Macherey, J. Klingner, A. Shah, M. Johnson, X. Liu, Ł. Kaiser, S. Gouws, Y. Kato, T. Kudo, H. Kazawa, K. Stevens, G. Kurian, N. Patil, W. Wang, C. Young, J. Smith, J. Riesa, A. Rudnick, O. Vinyals, G. Corrado, M. Hughes, and J. Dean, “Google’s Neural Machine Translation System: Bridging the Gap between Human and Machine Translation,” arXiv:1609.08144, 2016.
- [12] A. Graves, A. Mohamed, and G. Hinton, “Speech recognition with deep recurrent neural networks,” Proc. of the 2013 IEEE Int. Conf. on Acoustics, Speech and Signal Processing, pp. 6645-6649, 2013.
- [13] S. Hochreiter and J. Schmidhuber, “Long Short-Term Memory,” Neural Computation, Vol.9, Issue 8, pp. 1735-1780, 1997.
- [14] K. Cho, B. v. Merriënboer, C. Gulcehre, D. Bahdanau, F. Bougares, H. Schwenk, and Y. Bengio, “Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation,” arXiv: 1406.1078, 2014.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.