Paper:
Forecasting Realized Volatility in Financial Markets Based on a Time-Varying Non-Parametric Model
Wentao Gu*,†, Zhongdi Liu*, Cui Dong*, Jian He*, and Ming-Chuan Hsieh**
*School of Statistics and Mathematics, Zhejiang Gongshang University
18 Xuezheng Street, Xiasha Education Park, Hangzhou, Zhejiang 310018, China
†Corresponding author
**Research Center for Testing and Assessment, National Academy for Educational Research
No.2 Sanshu Road, Sanxia District, New Taipei City 23703, Taiwan
This paper proposes a new non-parametric adaptive combination model for the prediction of realized volatility on the basis of applying and extending the time-varying probability density function theory. We initially construct an adaptive time-varying weight mechanism for a combination forecast. To compare the predictive power of the models, we take the SPA test, which uses bootstrap as the evaluation criterion and employs the rolling window strategy for out-of-sample forecasting. The empirical study shows that the non-parametric TVF model forecasts more accurately than the HAR-RV model. In addition, the average combination forecast model does not have a significant advantage over any single model while our adaptive combination model does.
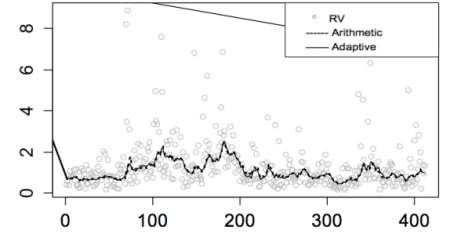
The predictive performance of the arithmetic average and adaptive combination forecast models
- [1] Q. Fu and X.-L.Wu, “Risk Research for Chinese Stock Market Based on ARFIMA-WRBV-VaR Model,” J. of Southwest University: Natural Science Edition, Vol.35, No.3, pp. 9-14, 2013 (in Chinese).
- [2] Ö. Ceylan, “Time-Varying Volatility Asymmetry: A Conditioned HAR-RV(CJ) EGARCH-M Model,” J. of Risk, Vol.17, No.2, pp. 21-49, 2014.
- [3] P. R. Hansen, Z. Huang, and H. H. Shek, “Realized GARCH: a joint model for returns and realized measures of volatility,” J. of Applied Econometrics, Vol.27, Issue 6, pp. 877-906, 2012.
- [4] T. G. Andersen, T. Bollerslev, and F. X. Diebold, “Roughing It Up: Including Jump Components in the Measurement, Modeling, and Forecasting of Return Volatility,” The Review of Economics and Statistics, Vol.89, Issue 4, pp. 701-720, 2007.
- [5] D. P. Louzis, S. Xanthopoulos-Sisinis, and A. N. Refenes, “Forecasting Stock Index Realized Volatility with an Asymmetric HAR-FIGARCH Model: The Case of S&P 500 and DJI Stock Indices,” SSRN, doi:10.2139/ssrn.1524861, 2010.
- [6] F. M. Bandi, J. R. Russell, and C. Yang, “Realized Volatility Forecasting in the Presence of Time-Varying Noise,” J. of Business & Economic Statistics, Vol.31, Issue 3, pp. 331-345, 2013.
- [7] B. Sévi, “Forecasting the volatility of crude oil futures using intraday data,” European J. of Operational Research, Vol.235, Issue 3, pp. 643-659, 2014.
- [8] A. Harvey and V. Oryshchenko, “Kernel density estimation for time series data,” Int. J. of Forecasting, Vol.28, Issue 1, pp. 3-14, 2012.
- [9] T. G. Andersen and T. Bollerslev, “Answering the Skeptics: Yes, Standard Volatility Models do Provide Accurate Forecasts,” Int. Economic Review, Vol.39, No.4, pp. 885-905, 1998.
- [10] P. R. Hansen and A. Lunde, “Realized Variance and Market Microstructure Noise,” J. of Business & Economic Statistics, Vol.24, Issue 2, pp. 127-161, 2006.
- [11] W. K. Newey and K. D. West, “Automatic Lag Selection in Covariance Matrix Estimation,” The Review of Economic Studies, Vol.61, No.4, pp. 631-653, 1994.
- [12] Z. Feng and Q. Ren, “Forecasting model with dynamical combined residual error correction,” Systems Engineering – Theory & Practice, Vol.37, No.7, pp. 1884-1991, 2017 (in Chinese).
- [13] P. R. Hansen, “A Test for Superior Predictive Ability,” J. of Business & Economic Statistics, Vol.23, Issue 4, pp. 365-380, 2005.
- [14] P. R. Hansen and A. Lunde, “A forecast comparison of volatility models: does anything beat a GARCH(1,1)?,” J. of Applied Econometrics, Vol.20, Issue 7, pp. 873-889, 2005.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.