Paper:
A Kansei-Based Sound Modulation System for Musical Instruments by Using Neural Networks
Daisuke Tanaka*, Ryuto Suzuki**, and Shigeru Kato*
*National Institute of Technology, Niihama College
7-1 Yagumo, Niihama, Ehime 792-8580, Japan
**The University of Electro-Communications
1-5-1 Chofugaoka, Chofu, Tokyo 182-8585, Japan
This study describes a sound modulation system based on the use of a neural network model. The inputs to the model are a) a basic, original sound wave, and b) the degree of Kansei, while the output of the model is modulated sound depending on the degree of Kansei. The degree of Kansei is the numerical value that expresses the modulation level based on a Kansei linguistic expression, such as hardness or brilliance. In the experiment, the models are constructed for the sounds of piano and Marimba. Three types of training data are used for each sound, and the degree of Kansei is assigned manually for each dataset. By changing the degree of Kansei at the input of the model, we have validated that each model could appropriately modulate the basic sound. In addition, the modulation results are illustrated for one octave of piano sounds. The potential of our proposed model and future work are also discussed.
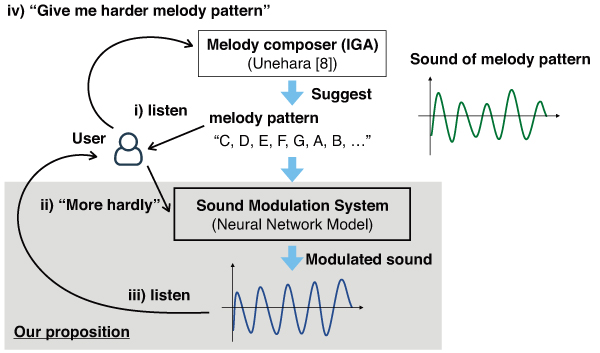
Concept of our model
- [1] M. Unehara and T. Onisawa, “Music composition system with human evaluation as human centered system,” Soft Computing, Vol.7, No.3, pp. 167-178, 2003.
- [2] M. Nagamachi, “Kansei Engineering: A new ergonomic consumer-oriented technology for product development,” Int. J. of Industrial Ergonomics, Vol.15, No.1, pp. 3-11, 1995.
- [3] H. Takagi, “Interactive evolutionary computation: fusion of the capabilities of EC optimization and human evaluation,” Proc. of the IEEE, Vol.89, No.9, pp. 1275-1296, 2001.
- [4] L. A. Zadeh, “Fuzzy sets,” Information and Control, Vol.8, No.3, pp. 338-353, 1965.
- [5] D. E. Rumelhart, G. E. Hinton, and R. J. Williams, “Learning representations by back-propagating errors,” Nature, Vol.323, pp. 533-536, 1986.
- [6] J. Chabassier, A. Chaigne, and P. Joly, “Modeling and simulation of a grand piano,” The J. of the Acoustical Society of America, Vol.134, No.1, pp. 648-665, 2013.
- [7] M. Nagahara and Y. Yamamoto, “H∞-Optimal Fractional Delay Filters with Application to Pitch Shifting,” IFAC Proc. Volumes, 10th IFAC Workshop on Time Delay Systems, Vol.45, No.14, pp. 61-66, 2012.
- [8] S. Kato, D. Tanaka, and R. Suzuki, “Affective Sound Modulation of Musical Instruments by using Neural Networks,” Proc. of 18th Int. Symp. on Advanced Intelligent Systems (ISIS2017), pp. 417-424, 2017.
- [9] The University of IOWA electronic music studios, “Musical Instrument Samples,” http://theremin.music.uiowa.edu/MIS.html, [accessed January 20, 2018]
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.