Short Paper:
A Correlation Evaluation Method for Complex Objects
Huan Wang*, Qingyuan Meng*, Min Ouyang**, and Ruishi Liang*
*Zhongshan Institute, University of Electronic Science and Technology of China
No.1 Xueyuan Road, Shiqi District, Zhongshan, Guangdong 528400, China
**Key Laboratory of Intelligent Information Perception and Processing Technology
No.88 Taishan Road, Tianyuan District, Zhuzhou, Hunan 412008, China
Data correlation evaluation is the basis for data analysis, and the academic community has proposed many indicators to evaluate it, such as the Euclidean distance, and angle cosine, and so on. However, it is difficult for these indicators to effectively express the correlation degree of complex objects. Using traffic intersections as an example, this article proposes an effective method to evaluate the correlation between complex objects. First, based on a large quantity of basic data, a standard data format describing traffic intersection attributes was proposed. Then, experienced engineers were asked to grade the correlation between intersections. Finally, the two intersection standard format datasets were used as model inputs, the engineer correlation rating as the output of the model, and the support vector machine model was employed for training. The results of this data experiment demonstrate that the trained model can effectively express the correlation degree between traffic intersections, and therefore proves the validity of the method.
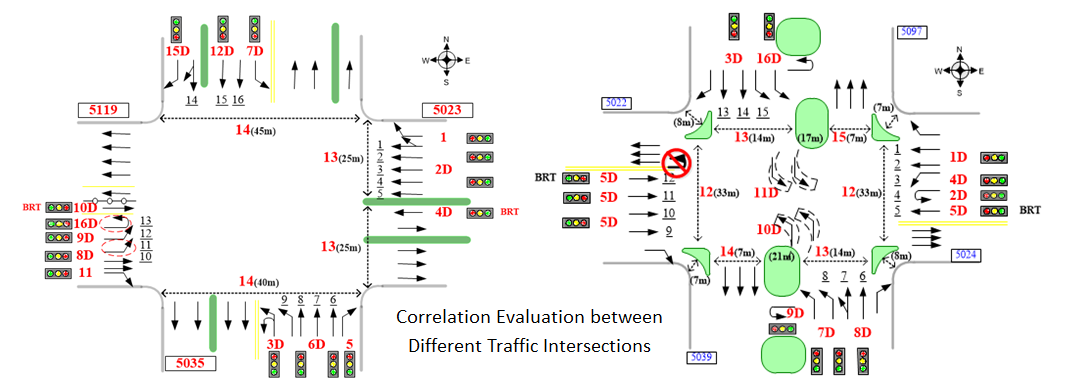
Correlation evaluation bewteen complex objects
- [1] C. Gan, W. Cao, M. Wu, et al., “Intelligent Nadaboost-ELM Modeling Method for Formation Drillability Using Well Logging Data,” J. Adv. Comput. Intell. Intell. Inform., Vol.20, No.7, pp. 1103-1111, 2016.
- [2] H. T. P. Thanh and P. Meesad, “Stock Market Trend Prediction Based on Text Mining of CorporateWeb and Time Series Data,” J. Adv. Comput. Intell. Intell. Inform., Vol.18, No.1, pp. 22-31, 2014.
- [3] S. Y. Li, Z. X. Mei, R. H. Zhang, et al., “Analyze of Spatial Characteristics and Its Influencing Factors of China’s Interprovincial Migration,” J. of South China Normal University (Natural Science Edition), Vol.49, No.3, pp. 84-91, 2017.
- [4] W. Z. Yu and H. T. Liu, “Correlation Between UrbaIlization and Climate Change of Shenzhen in Nearly 35 Years,” J. of South China Normal University (Natural Science Edition), Vol.50, No.1, pp. 85-91, 2018.
- [5] J. Draisma, G. Ottaviani, B. Sturmfels, et al., “The Euclidean Distance Degree of an Algebraic Variety,” Foundations of Computational Mathematics, Vol.16, No.1, pp. 99-149, 2016.
- [6] L. Liberti, C. Lavor, N. Maculan, et al., “Euclidean distance geometry and applications,” Quantitative Biology, Vol.56, No.1, pp. 3-69, 2012.
- [7] G. Kou and C. Lin, “A cosine maximization method for the priority vector derivation in AHP,” European J. of Operational Research, Vol.235, No.1, pp. 225-232, 2014.
- [8] A. Song, S. Cao, and J. Yao, “Quantitative evaluation of complex electromagnetic environment complexity based on a method of the cosine vector included angle,” IEEE Int. Conf. on Electronic Measurement & Instruments, pp. 320-323, 2016.
- [9] H. Liu, D. Guo, and F. Sun, “Object Recognition Using Tactile Measurements: Kernel Sparse Coding Methods,” IEEE Trans. on Instrumentation & Measurement, Vol.65, No.3, pp. 656-665, 2016.
- [10] I. N. Junejo, E. Dexter, I. Laptev, et al., “View-Independent Action Recognition from Temporal Self-Similarities,” IEEE Trans. on Pattern Analysis & Machine Intelligence, Vol.33, No.1, pp. 172-185, 2011.
- [11] M. Bermudez-Edo, P. Barnaghi, and K. Moessner, “Analysing real world data streams with spatio-temporal correlations: Entropy vs. Pearson correlation,” Automation in Construction, Vol.88, pp. 87-100, 2018.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.