Top > JACIII > Stability Regions of Nonlinear LCL-Filtered Converter with Con ...

single-jc.php

JACIII Vol.22 No.5 pp. 629-639
doi: 10.20965/jaciii.2018.p0629
(2018)

Paper:

Views over last 60 days: 865

Stability Regions of Nonlinear LCL-Filtered Converter with Converter-Current-Feedback Control Without Damping

Qingyi Wang*,**, Xuefen Wang*,**, Min Ding*,**,†, Quan Yin***, and Haichun Li***

*School of Automation, China University of Geosciences
No. 388, Lumo Road, Wuhan 430074, China

**Hubei Key Laboratory of Advanced Control and Intelligent Automation for Complex Systems
Wuhan 430074, China

***School of Automation, Huazhong University of Science and Technology
1037 Luoyu Road, Wuhan 430074, China

†Corresponding author

Received:
February 28, 2018
Accepted:
May 21, 2018
Published:
September 20, 2018
Creative Commons License
Keywords:
converter, nonlinear LCL-filtered model, stable boundaries, undamping
Abstract

The stability regions of a LCL-filtered converter adopting converter-current-feedback control without damping are analyzed. The nonlinear LCL-filtered model is presented to investigate its influence on the system stability. The stability analysis is performed by means of the Nyquist diagram in s domain. It reveals that three factors have the dominant effects on the system stability, including internal loss of LCL-filtered model, PWM transport delay and controller parameters. The undamped stability boundaries of the system gain calculated by the symmetrical optimum method are obtained. It can be found that stable regions for the nonlinear LCL-filtered system are extended into a continuous region of ratios of LCL filter resonance frequency to control frequency from three distinct regions. Finally, the stable regions are validated by the nonlinear model simulation, and experimental results verify the theoretical analysis.

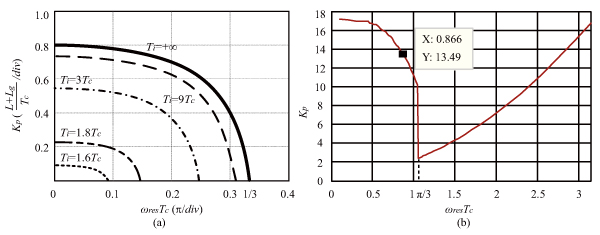
Nonlinear LCL-filtered system stability regions are extended into three distinct regions

Nonlinear LCL-filtered system stability regions are extended into three distinct regions

Cite this article as:
Q. Wang, X. Wang, M. Ding, Q. Yin, and H. Li, “Stability Regions of Nonlinear LCL-Filtered Converter with Converter-Current-Feedback Control Without Damping,” J. Adv. Comput. Intell. Intell. Inform., Vol.22 No.5, pp. 629-639, 2018.
Data files:
References
  1. [1] Q. Zhang, L. Qian, C. Zhang, and D. Cartes, “Study On Grid Connected Inverter Used in High Power Wind Generation System,” IEEE Industry Applications Conf. Forty-First IAS Annual Meeting (IAS), October, 2006.
  2. [2] M. Liserre, F. Blaabjerg, and S. Hansen, “Design and control of an LCL-filter-based three-phase active rectifier,” IEEE Trans. Indust. Appl., Vol.41, No.5, pp. 1281-1291, 2005.
  3. [3] J. Dannehl, M. Liserre, and F. W. Fuchs, “Filter-based active damping of voltage source converters with LCL filter,” IEEE Trans. Indust. Electron., Vol.58, No.8, pp. 3623-3633, 2011.
  4. [4] A. K. Balasubramanian and V. John, “Analysis and design of split-capacitor resistive-inductive passive damping for LCL filters in grid-connected inverters,” IET. Power Electron., Vol.6, No.9, pp. 1822-1832, 2013.
  5. [5] X. Wang, R. Beres, F. Blaabjerg, and P. C.Loh, “Passivity-based design of passive damping for LC-filtered voltage source converters,” IEEE Energy Conversion Congress and Exposition, Montreal, Canada, 2015.
  6. [6] C. Bao, X. Ruan, X. Wang, W. Li, D. Pan, and K. Weng, “Step-by-step controller design for LCL-type grid-connected inverter with capacitor-current-feedback active-damping,” IEEE Trans. Power Electron., Vol.29, No.3, pp. 1239-1253, 2014.
  7. [7] J. Dannehl, F. W. Fuchs, S. Hansen, and P. B. Thogersen, “Investigation of active damping approaches for PI-based current control of grid-connected pulse width modulation converters with LCL filters,” IEEE Trans. Indust. Appl., Vol.46, No.4, pp. 1509-1517, 2010.
  8. [8] F. Wang, J. L. Duarte, Marcel A. M. Hendrix, and P. F. Ribeiro, “Modeling and analysis of grid harmonic distortion impact of aggregated DG inverters,” IEEE Trans. Power Electron., Vol.26, No.3, pp. 786-797, 2011.
  9. [9] Z. Xin, X. Wang, P. C. Loh, and F. Blaabjerg, “Digital realization of capacitor-voltage feedback active damping for LCL-filtered grid converters,” IEEE Energy Conversion Congress and Exposition (ECCE), pp. 2690-2697, 2015.
  10. [10] Y. Huang, H. Wang, X. Zhang, and L. Gao, “Active damping-based control for grid-connected LCL-filtered inverter with capacitor voltage inertial feedback,” Proc. of 8th Int. Power Electronics and Motion Control Conf., Hefei, China, 2016.
  11. [11] N. Mukherjee and D. De, “Analysis and improvement of performance in LCL filter-based PWM rectifier/inverter application using hybrid damping approach,” IET. Power Electron., Vol.6, No.2, pp. 309-325, 2013.
  12. [12] Y. Lei, W. Xu, C. Mu et al., “New hybrid damping strategy for grid-connected photovoltaic inverter with LCL filter,” IEEE Trans. On Applied Superconductivity, Vol.24, No.5, pp. 1-8, 2014.
  13. [13] M. Wang, H. Lin, F. Gong et al., “Stability control for LC-L filter based load side converter of BDFG ship shaft power generation system without extra damping,” IEEE Energy Conversion Congress and Exposition (ECCE), 2015.
  14. [14] Y. Tang, P. C. Loh, P. Wang, F. H. Choo, and F. Gao, “Exploring inherent damping characteristic of LCL-filters for three-phase gird-connected voltage source inverters,” IEEE Trans. Power Electron., Vol.27, No.3, pp. 1433-1443, 2012.
  15. [15] C. Zou, B. Liu, S. Duan, and R. Li, “Influence of delay on system stability and delay optimization of grid-connected inverters with LCL filter,” IEEE Trans. Indust. Inform., Vol.10, No.3, pp. 1775-1784, 2014.
  16. [16] D. Pan, X. Ruan, C. Bao et al., “Capacitor-current-feedback active damping with reduced computation delay for improving robustness of LCL-type grid-connected inverter,” IEEE Trans Indust. Electron., Vol.29, No.7, pp. 3414-3427, 2014.
  17. [17] H. Safamehr, T. A. Najafabadi, and F. R. Salmasi, “Enhanced control of grid-connected inverters with non-linear inductor in LCL filter,” IET. Power Electron., Vol.9, No.10, pp. 2111-2120, 2016.
  18. [18] Y. Lyu, H. Lin, and Y. Cui, “Stability analysis of digitally controlled LCL-type grid-connected inverter considering the delay effect,” IET. Power Electron., Vol.8, No.9, pp. 1651-1660, 2015.
  19. [19] S. G. Parker, B. P. McGrath, and D. G. Holmes, “Regions of active damping control for LCL filters,” IEEE Trans. Ind. Appl., Vol.50, No,1, pp. 424-432, 2014.
  20. [20] J. Dannehl, C. Wessels, and F. W. Fuchs, “Limitations of voltage-oriented PI current control of grid-connected PWM rectifiers with LCL filters,” IEEE Trans. Ind. Electron., Vol.56, No.2, pp. 380-388, 2009.
  21. [21] S. Zurek, F. A. Naemi, and A. J. Moses, “Finite-element modeling and measurements of flux and eddy curremt distribution in toroidal cores wound from electrical steel,” IEEE Trans. on Magnetics, Vol.44, No.6, pp. 902-905, 2008.
  22. [22] D. Buecherl and H. G. Herzog, “Iron loss modeling by complex inductance for steady state simulation of electrical machines,” Int. Symp. on Power Electronics Electrical Drives Automation & Motion, 2010.
  23. [23] M. Ranta, M. Hinkkanen, A. Belahcen, and J. Luomi, “Inclusion of hysteresis and eddy current losses in nonlinear time-domain inductance models,” Conf. of the IEEE Industrial Electronics Society, Vol.6854, No.5, pp. 1897-1902, 2011.
  24. [24] D. Woodburn, T. Wu, L. Chow, and Q. Leland, “Novel nonlinear inductance modeling of permanent magnet motor,” IEEE Energy Conversion Congress & Exposition, 2013.
  25. [25] C. Jaschke, and P. Schegner, “Analytic computation of the magnetizing inductance of current instrument transformers under consideration of eddy current,” IEEE Trans. on Magnetics, Vol.51, No.11, pp. 1-4, 2015.
  26. [26] Z. Tian, X. Gao, B. Gong, and T. Shi. “Time-delay compensation method for networked control system based on time-delay prediction and implicit PIGPC,” Int. J. of Automation and Computing, Vol.12, No.6, pp. 648-656, 2015.
  27. [27] Z. Xin, X. Wang, P. C. Loh, and F. Blaabjerg, “Grid-current-feedback control for LCL-filtered grid converters with enhanced stability,” IEEE Trans. Power Electron., Vol.32, No.4, pp. 3216-3228, 2017.
  28. [28] Z. Tian, S. Li, Y. Wang, and Q. Zhang, “Multi permanent magnet synchronous motor synchronization control based on variable universe fuzzy PI method,” Engineering Letters, Vol.23, No.3, pp. 180-188, 2015.
  29. [29] X. Fu, and S. Li, “Control of single-phase grid-connected converters with LCL filters using recurrent neural network and conventional control methods,” IEEE Trans. on Power Electronics, Vol.31, No.7, pp. 5354-5364, 2016.
  30. [30] B. Terzic, G. Majic, and A. Slutej, “Stability analysis of three-phase PWM converter with LCL filter by means of nonlinear model,” AUTOMATIKA, Vol.51, No.3, pp. 221-232, 2010.
  31. [31] J. Yin, S. Duan, and B. Liu, “Stability analysis of grid-connected inverter with LCL filter adopting a digital single-loop controller with inherent damping characteristic,” IEEE Trans. Indust. Inform., Vol.9, No.2, pp. 1104-1112, 2013.
  32. [32] X. Wang, F.Blaabjerg, and W. Wu, “Modeling and analysis of harmonic stability in an AC power-electronics-based power system,” IEEE Trans. Power Electron., Vol.29, No.12, pp. 6421-6432, 2014.
  33. [33] W. Gong, S. Hu, M. Shan, and H. Xu, “Robust current control design of a three phase voltage source converter,” J. of Modeling Power System and Clean Energy, Vol.2, No.1, pp. 16-22, 2014.
  34. [34] D. M. Van de Sype, K. D. Gusseme, F. D. Belie, A. P. Van den Bossche, and J. A. Melkebeek, “Small-signal z-domain analysis of digitally controlled converters,” IEEE Trans. Power Electron., Vol.21, No.2, pp. 470-478, 2006.
  35. [35] J. Wang, J. D. Yan, L. Jiang, and J. Zou, “Delay-dependent stability of single-loop controlled grid-connected inverters with LCL filters,” IEEE Trans. Power Electron., Vol.31, No.1, pp. 743-757, 2016.

Creative Commons License  This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.

*This site is desgined based on HTML5 and CSS3 for modern browsers, e.g. Chrome, Firefox, Safari, Edge, Opera.

Last updated on Apr. 22, 2024