Research Paper:
Type-2 Fuzzy Robust Regression with Two-Step Construction
Yoshiyuki Yabuuchi

Shimonoseki City University
2-1-1 Daigaku-cho, Shimonoseki, Yamaguchi 751-8510, Japan
Regression models that describe the relationship between independent and dependent variables are widely used owing to their simple structure, ease of handling, and ease of interpretation. One such model is the interval fuzzy regression model that uses fuzzy sets. This model represents the possibility distribution of an analysis target in terms of interval predictions. Generally, the vagueness of a dependent variable is represented by the intervals of type-1 fuzzy sets. However, these observations contain errors, and the interval predictions are considered vague. Therefore, research has been conducted on fuzzy regression using type-2 fuzzy sets. A type-2 fuzzy regression model has been proposed to illustrate possibility distribution of an analysis target through possibilistic and necessity regressions. To investigate reliable and robust fuzzy regression models, this study constructs a type-2 fuzzy robust regression model for possibilistic regression, which illustrates the possibility distribution of the analyte, and a fuzzy robust regression model, which illustrates the robust possibility of the analyte. Numerical examples are used to confirm the characteristics of the proposed model and identify future research directions.
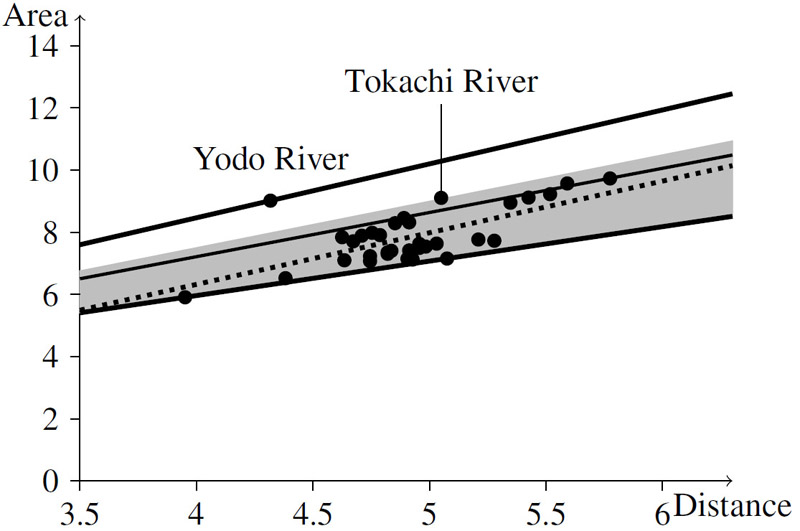
Type-2 fuzzy robust regression
- [1] R. Coppi, P. D’Urso, P. Giordani, and A. Santoro, “Least squares estimation of a linear regression model with LR fuzzy response,” Computational Statistics & Data Analysis, Vol.51, Issue 1, pp. 267-286, 2006. https://doi.org/10.1016/j.csda.2006.04.036
- [2] P. Diamond, “Fuzzy Least Squares,” Information Science, Vol.46, Issue 3, pp. 141-157, 1988. https://doi.org/10.1016/0020-0255(88)90047-3
- [3] M. Modarres, E. Nasrabadi, and M. M. Nasrabadi, “Fuzzy linear regression model with least square errors,” Applied Mathematics and Computation, Vol.163, Issue 2, pp. 977-989, 2005. https://doi.org/10.1016/j.amc.2004.05.004
- [4] A. A. Ramli, J. Watada, and W. Pedrycz, “Real-time fuzzy regression analysis: A convex hull approach,” European J. of Operational Research, Vol.210, Issue 3, pp. 606-617, 2011. https://doi.org/10.1016/j.ejor.2010.10.007
- [5] A. A. Ramli, J. Watada, and W. Pedrycz, “A Combination of Genetic Algorithm-based Fuzzy C-Means with a Convex Hull-based Regression for Real-Time Fuzzy Switching Regression Analysis: Application to Industrial Intelligent Data Analysis,” IEEJ Trans. on Electrical and Electronic Engineering, Vol.9, Issue 1, pp. 71-82, 2014. https://doi.org/10.1002/tee.21938
- [6] Y. Yabuuchi and J. Watada, “Building Fuzzy Robust Regression Model Based on Granularity and Possibility Distribution,” W. Pedrycz and S.-M. Chen (Eds.), “Information Granularity, Big Data, and Computational Intelligence,” Springer-Verlag Berlin Heidelberg, pp. 247-272, 2014. https://doi.org/10.1007/978-3-319-08254-7_12
- [7] Y. Wei and J. Watada, “Building a type-2 fuzzy regression model based on creditability theory,” Proc. IEEE Int. Conf. on Fuzzy Systems (FUZZ-IEEE 2013), 2013. https://doi.org/10.1109/fuzz-ieee.2013.6622562
- [8] Y. Wei and J. Watada, “Building a type-2 fuzzy regression model based on credibility theory and its application on arbitrage pricing theory,” IEEJ Trans. on Electrical and Electronic Engineering, Vol.11, Issue 6, pp. 720-729, 2016. https://doi.org/10.1002/tee.22297
- [9] R. Almahasneh, B. Tüű-Szabó, L.T. Kóczy, and P. Földesi, “Optimization of the Time-Dependent Traveling Salesman Problem Using Interval-Valued Intuitionistic Fuzzy Sets,” Axioms, Vol.9, No.2, Article No.53, 2020. https://doi.org/10.3390/axioms9020053
- [10] Y. Chen, “Study on Centroid Type-Reduction of Interval Type-2 Fuzzy Logic Systems Based on Noniterative Algorithms,” Complexity, Vol.2019, Article No.7325053, 2019. https://doi.org/10.1155/2019/7325053
- [11] N. N. Karnik and J. M. Mendel, “Operations on type-2 fuzzy sets,” Fuzzy Sets and Systems, Vol.122, Issue 2, pp. 327-348, 2001. https://doi.org/10.1016/S0165-0114(00)00079-8
- [12] M. Ramírez and P. Melin, “A New Interval Type-2 Fuzzy Aggregation Approach for Combining Multiple Neural Networks in Clustering and Prediction of Time Series,” Int. J. of Fuzzy Systems, Vol.25, No.3, pp. 1077-1104, 2023. https://doi.org/10.1007/s40815-022-01426-5
- [13] H. Uesu, “Triangular Shaped Type-2 Fuzzy Number and Uesu Product,” Innovative Computing, Information and Control Express Letters (ICICEL), Vol.16, No.8, pp. 869-876, 2022. https://doi.org/10.24507/icicel.16.08.869
- [14] Y. Yabuuchi and J. Watada, “Fuzzy Robust Regression Model by Possibility Maximization,” J. Adv. Comput. Intell. Intell. Inform., Vol.15, No.4, pp. 479-484, 2011. https://doi.org/10.20965/jaciii.2011.p0479
- [15] Y. Yabuuchi, “Possibility Grades with Vagueness in Fuzzy Regression Models,” Procedia Computer Science, Vol.112, pp. 1470-1478, 2017. https://doi.org/10.1016/j.procs.2017.08.025
- [16] Y. Yabuuchi, “Fuzzy Regression Model Dealing with Vague Possibility Grades and Its Characteristics,” Proc. of 10th KES Int. Conf. on Intelligent Decision Technologies (KES-IDT 2018), pp. 98-108, 2018. https://doi.org/10.1007/978-3-319-92028-3_10
- [17] Y. Yabuuchi, “Type-2 Fuzzy Robust Regression Considering Vagueness of Membership Values,” Proc. 19th Int. Symposium on Management Engineering, 2024.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.