Paper:
Comparative Study of In-Phase and Anti-Phase Arm Swingings in Rimless Wheel Locomotion
Cong Yan*
 , Yanqiu Zheng**
, Yanqiu Zheng**
 , Fumihiko Asano***
, Fumihiko Asano***
 , and Isao Tokuda*
, and Isao Tokuda*

*Department of Mechanical Engineering, Ritsumeikan University
1-1-1 Nojihigashi, Kusatsu, Shiga 525-8577, Japan
**Department of Applied Electronics, Faculty of Advanced Engineering, Tokyo University of Science
6-3-1 Niijuku, Katsushika-ku, Tokyo 125-8585, Japan
***Graduate School of Advanced Science and Technology, Japan Advanced Institute of Science and Technology
1-1 Asahidai, Nomi, Ishikawa 923-1292, Japan
This paper investigated the dynamics and control of an underactuated rimless wheel (RW) with semicircular feet driven by two pendulum-like arms. We focused on the entrainment property of the RW walking to the periodic oscillations of the arms and analyzed how different arm coordination patterns, i.e., in-phase and anti-phase swingings, affect the walking stability and performance of the system. A mathematical model was developed that captured the continuous dynamics, collision events, and control method for this hybrid mechanical system. Numerical simulations demonstrated that the anti-phase arm swinging, similar to human walking, provided superior performance compared to the in-phase swinging. Specifically, the anti-phase coordination yielded a wider range of entrainment, as well as a wider range of stable walking, across various control parameters including the forcing frequency and the arm weight. Through rigorous Poincaré map stability analysis, we further quantified the system’s robustness to perturbations, revealing that anti-phase arm swinging maintains stability even with increased arm mass, while in-phase swinging becomes unstable. The stable walking of the anti-phase coordination was supported by the opposing movements of the left and right arms, which effectively counterbalance the forward and backward momentums to suppress the ground reaction forces. These results may provide design principles for controlling underactuated walking robots with arms.
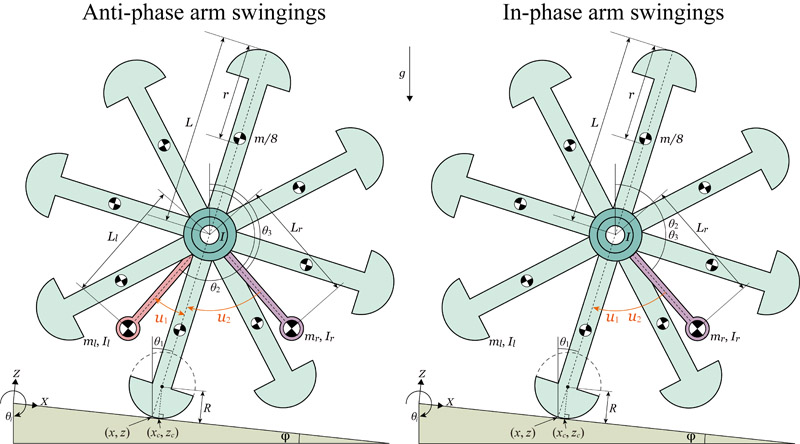
Anti-phase vs in-phase arm swingings
- [1] T. McGeer et al., “Passive dynamic walking,” Int. J. Robotics Res., Vol.9, No.2, pp. 62-82, 1990. https://doi.org/10.1177/027836499000900206
- [2] T. McGeer, “Dynamics and control of bipedal locomotion,” J. of Theoretical Biology, Vol.163, No.3, pp. 277-314, 1993. https://doi.org/10.1006/jtbi.1993.1121
- [3] S. Collins, A. Ruina, R. Tedrake, and M. Wisse, “Efficient bipedal robots based on passive-dynamic walkers,” Science, Vol.307, No.5712, pp. 1082-1085, 2005. https://doi.org/10.1126/science.1107799
- [4] S. H. Collins and A. Ruina, “A bipedal walking robot with efficient and human-like gait,” Proc. of the 2005 IEEE Int. Conf. on Robotics and Automation, pp. 1983-1988, 2005. https://doi.org/10.1109/ROBOT.2005.1570404
- [5] M. J. Coleman, A. Chatterjee, and A. Ruina, “Motions of a rimless spoked wheel: A simple three-dimensional system with impacts,” Dynamics and Stability of Systems, Vol.12, No.3, pp. 139-159, 1997. https://doi.org/10.1080/02681119708806242
- [6] F. Asano and Z.-W. Luo, “Asymptotically stable biped gait generation based on stability principle of rimless wheel,” Robotica, Vol.27, No.6, pp. 949-958, 2009. https://doi.org/10.1017/S0263574709005372
- [7] F. Asano, Y. Zheng, and X. Xiao, “Time-scale control approaches to collisionless walking of an underactuated rimless wheel,” J. Robot. Mechatron., Vol.29, No.3, pp. 471-479, 2017. https://doi.org/10.20965/jrm.2017.p0471
- [8] Y. Kuramoto, “Chemical oscillations, waves, and turbulence,” Springer, 1984. https://doi.org/10.1007/978-3-642-69689-3
- [9] A. Pikovsky, M. Rosenblum, and J. Kurths, “Synchronization: A universal concept in nonlinear sciences,” Cambridge University Press, 2001. https://doi.org/10.1017/CBO9780511755743
- [10] S. Strogatz, “Synchronization: A universal concept in nonlinear sciences,” Physics Today, Vol.56, No.1, p. 47, 2003. https://doi.org/10.1063/1.1554136
- [11] J. Ahn and N. Hogan, “Walking is not like reaching: evidence from periodic mechanical perturbations,” PloS one, Vol.7, No.3, Article No.e31767, 2012. https://doi.org/10.1371/journal.pone.0031767
- [12] F. Asano and I. Tokuda, “Indirectly controlled limit cycle walking of combined rimless wheel based on entrainment to active wobbling motion,” Multibody System Dynamics, Vol.34, pp. 191-210, 2015. https://doi.org/10.1007/s11044-014-9419-6
- [13] Y. Hanazawa, T. Hayashi, M. Yamakita, and F. Asano, “High-speed limit cycle walking for biped robots using active up-and-down motion control of wobbling mass,” 2013 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, pp. 3649-3654, 2013. https://doi.org/10.1109/IROS.2013.6696877
- [14] Y. Hanazawa and F. Asano, “High-speed biped walking using swinging-arms based on principle of up-and-down wobbling mass,” 2015 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 5191-5196, 2015. https://doi.org/10.1109/ICRA.2015.7139922
- [15] H. Pontzer, J. H. Holloway 4th, D. A. Raichlen, and D. E. Lieberman, “Control and function of arm swing in human walking and running,” J. of Experimental Biology, Vol.212, No.4, pp. 523-534, 2009. https://doi.org/10.1242/jeb.024927
- [16] S. H. Collins, P. G. Adamczyk, and A. D. Kuo, “Dynamic arm swinging in human walking,” Proc. of the Royal Society B: Biological Sciences, Vol.276, No.1673, pp. 3679-3688, 2009. https://doi.org/10.1098/rspb.2009.0664
- [17] S. M. Bruijn, O. G. Meijer, P. J. Beek, and J. H. Van Dieen, “The effects of arm swing on human gait stability,” J. of Experimental Biology, Vol.213, No.23, pp. 3945-3952, 2010. https://doi.org/10.1242/jeb.045112
- [18] J. Park, “Synthesis of natural arm swing motion in human bipedal walking,” J. of Biomechanics, Vol.41, No.7, pp. 1417-1426, 2008. https://doi.org/10.1016/j.jbiomech.2008.02.031
- [19] A. Goswami, B. Thuilot, and B. Espiau, “Compass-like biped robot part i: Stability and bifurcation of passive gaits,” Ph.D. dissertation, INRIA, 1996.
- [20] C. Yan, L. Li, W. Yanagimoto, Z. Feng, and I. Tokuda, “Modeling and optimization of an arc-shaped sliding locomotion robot with wobbling mass,” J. Robot. Mechatron., Vol.35, No.4, pp. 1063-1072, 2023. https://doi.org/10.20965/jrm.2023.p1063
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.