Paper:
Coverage Control with Multi-Leader and Follower Systems
Ryosuke Morita
 and Hideaki Muraji
and Hideaki Muraji
Gifu University
1-1 Yanagido, Gifu, Gifu 501-1193, Japan
This study proposes a hierarchical coverage control method customized for heterogeneous multi-agent systems. In the proposed framework, agents are divided into leaders and followers. The leaders perform computationally intensive centroidal Voronoi control, whereas the followers track their assigned leaders using lightweight local rules. This division of roles addresses the challenge of the high computational demand of conventional coverage algorithms, thus making the method suitable for systems with limited onboard processing capabilities. Simulation results show that the proposed method significantly reduces computational load while achieving similar or superior coverage performance compared with conventional methods, even under non-uniform spatial importance distributions. The results demonstrate the feasibility of scalable and efficient coverage control for heterogeneous agents and indicate its applicability to real-world scenarios such as environmental monitoring and disaster response.
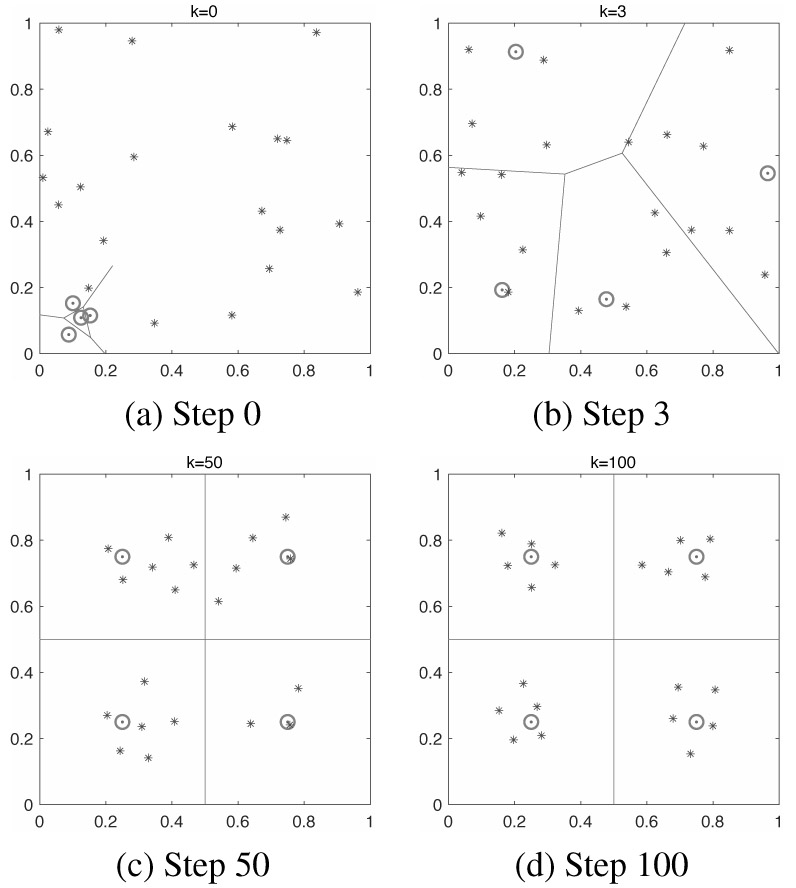
Simulation result obtained using the proposed method
- [1] I. F. Akyildiz, W. Su, Y. Sankarasubramaniam, and E. Cayirci, “Wireless sensor networks: A survey,” Computer Networks, Vol.38, No.4, pp. 393-422, 2002. https://doi.org/10.1016/S1389-1286(01)00302-4
- [2] N. Michael, J. Fink, and V. Kumar, “Cooperative manipulation and transportation with aerial robots,” Autonomous Robots, Vol.30, No.1, pp. 73-86, 2011. https://doi.org/10.1007/s10514-010-9205-0
- [3] R. Olfati-Saber, J. A. Fax, and R. M. Murray, “Consensus and cooperation in networked multi-agent systems,” Proc. of the IEEE, Vol.95, No.1, pp. 215-233, 2007. https://doi.org/10.1109/JPROC.2006.887293
- [4] F, Bullo, J. Cortés, and S. Martínez, “Distributed Control of Robotic Networks,” Princeton University Press, 2009.
- [5] D. H. Nguyen and S. Hara, “Hierarchical decentralized controller synthesis for heterogeneous Multi-agent dynamical system by LQR,” SICE J. of Control, Measurement, and System Integration, Vol.8, No.4, pp. 295-302, 2021. https://doi.org/10.9746/jcmsi.8.295
- [6] S. Hara, J. Imura, K. Tsumura, T. Ishizaki, and T. Sadamoto, “Glocal (global/local) control synthesis for hierarchical networked systems,” Proc. 2015 IEEE Conf. on Control Applications, pp. 107-112, 2015. https://doi.org/10.1109/CCA.2015.7320618
- [7] Y. Kantaros and M. M. Zavlanos, “Distributed communication-aware coverage control by mobile sensor networks,” Automatica, Vol.63, pp. 209-220, 2016. https://doi.org/10.1016/j.automatica.2015.10.035
- [8] D. Tsubakino and R. Morita, “Hierarchical quasi-optimal control for multiple identical LTI subsystems with event-triggered cooperation,” Proc. 61st SICE Annual Conf., pp. 1278-1283, 2022. https://doi.org/10.23919/SICE56594.2022.9905801
- [9] S. Hara, H. Shimizu, and T.-H. Kim, “Consensus in Hierarchical Multi-Agent Dynamical Systems With Low-Rank Interconnections: Analysis of Stability and Convergence Rates,” Proc. 2009 American Control Conf., pp. 5192-5197, 2009. https://doi.org/10.1109/ACC.2009.5160572
- [10] K. Kobayashi, S. Ueno, and T. Higuchi, “Multi-robot patrol with continuous connectivity and assessment of base station situation awareness,” J. Robot. Mechatron., Vol.36, No.3, pp. 526-537, 2024. https://doi.org/10.20965/jrm.2024.p0526
- [11] Y. Sueoka, M. Okada, Y. Tsunoda, Y. Sugimoto, and K. Osuka, “Exploration of a simple navigation method for swarm robots pioneered by heterogeneity,” J. Robot. Mechatron., Vol.35, No.4, pp. 948-956, 2023. https://doi.org/10.20965/jrm.2023.p0948
- [12] D. H. Nguyen, “A sub-optimal consensus design for multi-agent systems based on hierarchical LQR,” Automatica, Vol.55, pp. 88-94, 2015. https://doi.org/10.1016/j.automatica.2015.02.037
- [13] C. B. Yu, Y. Q. Wang, and J. L. Shao, “Optimization of formation for multi-agent systems based on LQR,” Frontiers of Information Technology and Electronic Engineering, Vol.17, pp. 96-109, 2016. https://doi.org/10.1631/FITEE.1500490
- [14] D. V. Dimarogonas and K. J. Kyriakopoulos, “Inverse agreement protocols with application to distributed multi-agent dispersion,” IEEE Trans. on Automatic Control, Vol.54, No.3, pp. 657-663, 2009. https://doi.org/10.1109/TAC.2008.2011009
- [15] V. Gazi and K. M. Passino, “A class of attraction/repulsion functions for stable swarm aggregations,” Int. J. of Control, Vol.77, No.18, pp. 1567-1579, 2004. https://doi.org/10.1080/00207170412331330021
- [16] M. Schwager, D. Rus, and J.-J. E. Slotine, “Unifying geometric, probabilistic, and potential field approaches to multi-robot coverage control,” The Int. J. of Robotics Research, Vol.30, No.3, pp. 371-383, 2011. https://doi.org/10.1177/0278364910383444
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.