Paper:
Input-Constrained Human Assist Control for Automobiles Using Control Barrier Functions
Issei Tezuka*
 , Hisakazu Nakamura**
, Hisakazu Nakamura**
 , Takashi Hatano***
, Takashi Hatano***
 , Kenji Kamijo***, and Shota Sato***
, Kenji Kamijo***, and Shota Sato***

*Graduate School of Frontier Sciences, The University of Tokyo
5-1-5 Kashiwanoha, Kashiwa, Chiba 277-8561, Japan
**Department of Electrical Engineering, Faculty of Science and Technology, Tokyo University of Science
2641 Yamazaki, Noda, Chiba 278-8510, Japan
***Integrated Control System Development Division, Mazda Motor Corporation
3-1 Shinchi, Fuchu-cho, Aki-gun, Hiroshima 730-8670, Japan
Control barrier functions with the notion of viability kernels solve state-constrained problems under input constraints. However, it is not clear that how viability kernels are obtained for general systems and whether an optimal safety assist controller satisfying both state and input constraints is continuous. In this paper, we consider a four-wheeled vehicle model and demonstrate how to obtain its viability kernel. Then, by explicitly solving an optimization problem, we design a human assist controller that ensures the safety of the system with minimal intervention. Moreover, we show that the proposed explicit controller is continuous. Lastly, we confirm the effectiveness of the proposed method by computer simulation.
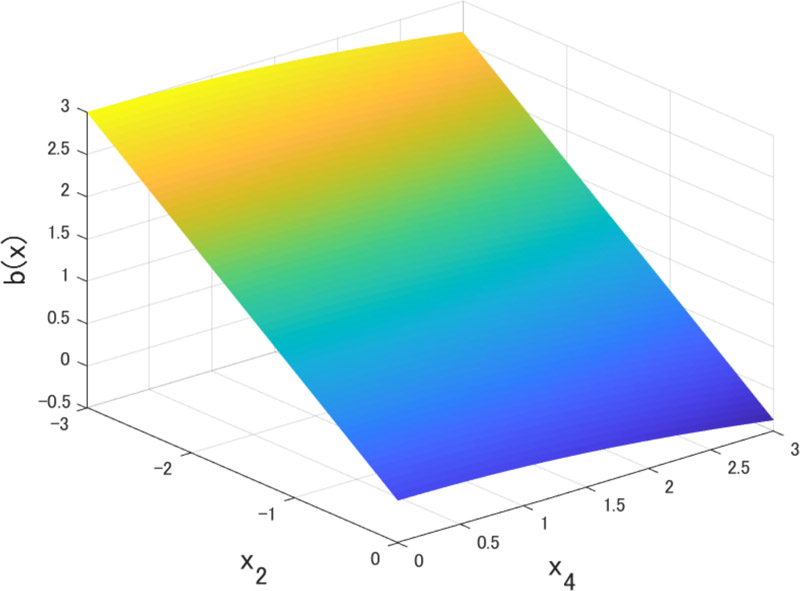
CBF for viability kernel
- [1] A. D. Ames, S. Coogan, M. Egerstedt, G. Notomista, K. Sreenath, and P. Tabuada, “Control barrier function: Theory and applications,” 18th European Control Conf. (ECC), pp. 3420-3431, 2019. https://doi.org/10.23919/ECC.2019.8796030
- [2] A. D. Ames, X. Xu, J. W. Grizzle, and P. Tabuada, “Control barrier function based quadratic programs for safety critical systems,” IEEE Trans. on Automatic Control, Vol.62, No.8, pp. 3861-3876, 2017. hhttps://doi.org/10.1109/TAC.2016.2638961
- [3] K. L. Hobbs, M. L. Mote, M. C. L. Abate, S. D. Coogan, and E. M. Feron, “Runtime assurance for safety-critical systems: An introduction to safety filtering approaches for complex control systems,” IEEE Control Systems Magazine, Vol.43, No.2, pp. 28-65, 2023. https://doi.org/10.1109/MCS.2023.3234380
- [4] W. Xiao and C. Belta, “High-order control barrier functions,” IEEE Trans. on Automatic Control, Vol.67, No.7, pp. 3655-3662, 2022. https://doi.org/10.1109/TAC.2021.3105491
- [5] M. Jankovic, “Why would we want a multi-agent system unstable,” Keynote Lecture, 2023 American Control Conf. (ACC), 2023.
- [6] Y. Huang, S. Z. Yong, and Y. Chen, “Guaranteed vehicle safety control using control-dependent barrier functions,” Proc. 2019 American Control Conf. (ACC), pp. 983-988, 2019. https://doi.org/10.23919/ACC.2019.8814761
- [7] Y. Chen, H. Peng, and J. Grizzle, “Obstacle avoidance for low-speed autonomous vehicles with barrier function,” IEEE Trans. on Control Systems Technology, Vol.26, No.1, pp. 194-206, 2018.
- [8] W. S. Cortez, D. Oetomo, C. Manzie, and P. Choong, “Control barrier functions for mechanical systems: theory and application to robotic grasping,” IEEE Trans. on Control Systems Technology, Vol.29, No.2, pp. 530-545, 2021. https://doi.org/10.1109/TCST.2019.2952317
- [9] P. Glotfelter, I. Buckley, and M. Egerstedt, “Hybrid nonsmooth barrier functions with applications to provably safe and composable collision avoidance for robotic systems,” IEEE Robotics and Automation Letters, Vol.4, No.2, pp. 1303-1310, 2019. https://doi.org/10.1109/LRA.2019.2895125
- [10] M. Srinivasan and S. Coogan, “Control of mobile robots using barrier functions under temporal logic specifications,” IEEE Trans. on Robotics, Vol.37, No.2, pp. 363-374, 2021. https://doi.org/10.1109/TRO.2020.3031254
- [11] D. R. Agrawal and D. Panagou, “Safe control synthesis via input constrained control barrier functions,” arXiv:2104.01704, 2021. https://doi.org/10.48550/arXiv.2104.01704
- [12] A. D. Ames, G. Notomista, Y. Wardi, and M. Egerstedt, “Integral control barrier functions for dynamically defined control laws,” IEEE Control Systems Letters, Vol.5, No.3, pp. 887-892, 2021. https://doi.org/10.1109/LCSYS.2020.3006764
- [13] K. Garg, R. K. Cosner, U. Rosolia, A. D. Ames, and D. Panagou, “Multi-rate control design under input constraints via fixed-time barrier functions,” IEEE Control Systems Letters, Vol.6, pp. 608-613, 2022. https://doi.org/10.1109/LCSYS.2021.3084322
- [14] A. Clark, “Verification and synthesis of control barrier functions,” 60th IEEE Conf. on Decision and Control (CDC 2021), pp. 6105-6112, 2021. https://doi.org/10.1109/CDC45484.2021.9683520
- [15] F. Blanchini, “Set invariance in control,” Automatica, Vol.35, No.11, pp. 1747-1767, 1999. https://doi.org/10.1016/S0005-1098(99)00113-2
- [16] I. Tezuka and H. Nakamura, “Strict zeroing control barrier function for continuous safety assist control,” IEEE Control Systems Letters, Vol.6, pp. 2108-2113, 2022. https://doi.org/10.1109/LCSYS.2021.3138526
- [17] M. Nagai and H. Yoshida, “Evolution and Evaluation of Safety Offered by Active Safety, ADAS, and AD Systems,” J. Robot. Mechatron., Vol.32, No.3, pp. 484-493, 2020. https://doi.org/10.20965/jrm.2020.p0484
- [18] M. Saito, H. Nakamura, T. Hayashi, and T. Yoshinaga, “Locally Semiconcave Control Barrier Function Design for Human Assist Control,” 45th Annual Conf. of the IEEE Industrial Electronics Society (IECON 2019), pp. 430-435, 2019. https://doi.org/10.1109/IECON.2019.8927572
- [19] I. Tezuka, H. Nakamura, T. Hatano, K. Kamijo, and S. Sato, “Input-constrained Human Assist Control via Control Barrier Function for Viability Kernel,” 2023 American Control Conf. (ACC), pp. 3921-3926, 2023. https://doi.org/10.23919/ACC55779.2023.10156411
- [20] J.-P. Aubin, A. M. Bayen, and P. Saint-Pierre, “Viability Theory: New Directions, Second Edition,” Springer-Verlag, 2011. https://doi.org/10.1007/978-3-642-16684-6
- [21] T. H. Gronwall, “Note on the derivatives with respect to a parameter of the solutions of a system of differential equations,” Annals of Mathematics, Vol.20, No.4, pp. 292-296, 1919. https://doi.org/10.2307/1967124
- [22] H. K. Khalil, “Nonlinear Systems, Third Edition,” Prentice Hall, 2002.
- [23] M. Maghenem and R. G. Sanfelice, “On the converse safety problem for differential inclusions: Solutions, regularity, and time-varying barrier functions,” IEEE Trans. on Automatic Control, Vol.68, No.1, pp. 172-187, 2023. https://doi.org/10.1109/TAC.2022.3144090
- [24] D. P. Bertsekas, “Nonlinear Programming, Second Edition,” Athena Scientific, 1999.
- [25] G. Teschl, “Ordinary Differential Equations and Dynamical Systems,” American Mathematical Society, 2012. https://doi.org/10.1090/gsm/140
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.