Paper:
Stability Conditions of Feedforward Control for a Musculoskeletal System with Muscles Whose Lengths Depend on Multiple Joint Angles
Koichi Komada*1
 , Kenshun Fujibe*2, Kazuyuki Tsuda*3, Hiroaki Ochi*4, and Hitoshi Kino*5
, Kenshun Fujibe*2, Kazuyuki Tsuda*3, Hiroaki Ochi*4, and Hitoshi Kino*5

*1Ritsumeikan Global Innovation Research Organization, Ritsumeikan University
1-1-1 Nojihigashi, Kusatsu, Shiga 525-8577, Japan
*2Department of Mechanical and System Engineering, Chukyo University
101-2 Yagoto Honmachi, Showa-ku, Nagoya, Aichi 466-8666, Japan
*3Kyushu Sangyo University
3-1 Matsukadai 2-chome, Higashi-ku, Fukuoka 813-8503, Japan
*4Division of Mechanical Engineering, Ashikaga University
268-1 Omae-cho, Ashikaga, Tochigi 326-8558, Japan
*5Department of Mechanical and System Engineering, Chukyo University
101-2 Yagoto Honmachi, Showa-ku, Nagoya, Aichi 466-8666, Japan
In this study, we consider a musculoskeletal system in which muscle tension is employed to control a linkage structure consisting of mechanical elements that correspond to a skeletal structure. Because muscles can only transmit force in the tensile direction, more muscles than joint degrees of freedom are needed to achieve control. The musculoskeletal potential method uses the potential field generated by the internal forces between muscles arising from this redundancy. In this method, constant muscle tension balanced at the desired posture is used as the step input to carry out feed forward control, in which sensory feedback and complex real-time computations are not required. However, the potential field generated by the muscle internal forces is highly dependent on muscular arrangement, some of which may fail to converge to the desired posture. For a musculoskeletal system with a specific structure consisting of two joints and six muscles, a previous study identified the conditions of the muscular arrangement required to achieve convergence to the desired posture. A further study analyzed the conditions of convergence for a more general multi-articular multimuscular system with several joints and muscles, although the joints were limited to a single degree of freedom and muscles to mono- and bi-articular ones, whose lengths were dependent on at most two adjacent joints. In this study, we consider cases consisting of joints with multiple degrees of freedom and muscles whose lengths depend on the angles of three or more joints. We mathematically analyze the conditions of convergence in the musculoskeletal potential method and verify the findings by simulation.
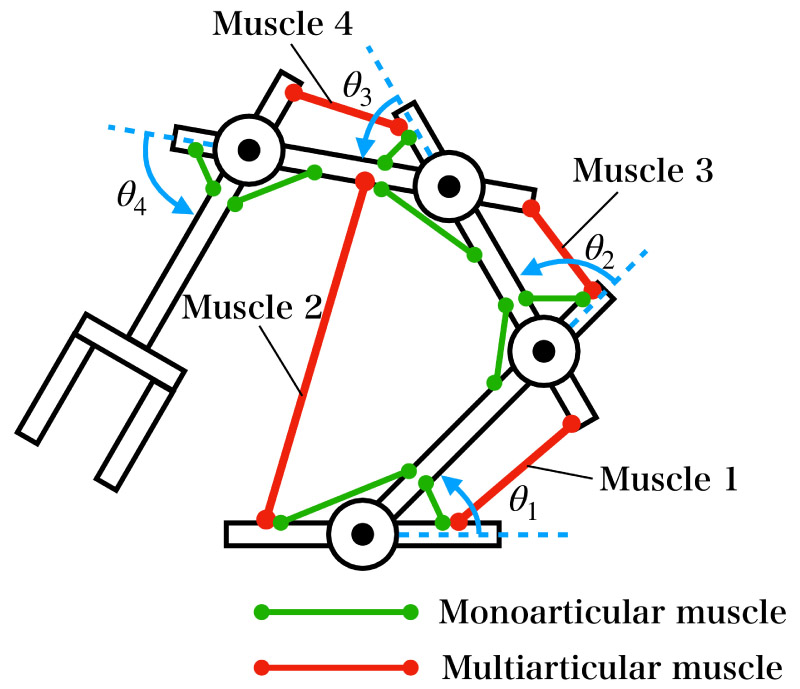
Musculoskeletal system with multi-articular muscles
- [1] H. Gomi and M. Kawato, “Human arm stiffness and equilibrium-point trajectory during multi-joint movement,” Biological Cybernetics, Vol.76, No.3, pp. 163-171, 1997. https://doi.org/10.1007/s004220050329
- [2] M. Kumamoto, T. Oshima, and T. Yamamoto, “Control properties induced by the existence of antagonistic pairs of bi-articular muscles – Mechanical engineering model analyses,” Human Movement Sci., Vol.13, Issue 5, pp. 611-634, 1994. https://doi.org/10.1016/0167-9457(94)90009-4
- [3] S. Hirose and S. Ma, “Redundancy decomposition control for multi-joint manipulator,” Proc. IEEE Int. Conf. on Robot. Automat., pp. 119-124, 1989. https://doi.org/10.1109/ROBOT.1989.99977
- [4] R. Ozawa, H. Kobayashi, and K. Hashirii, “Analysis, Classification, and Design of Tendon-Driven Mechanisms,” Trans. on Robot., Vol.30, Issue 2, pp. 396-410, 2014. https://doi.org/10.1109/TRO.2013.2287976
- [5] K. Koganezawa and Y. Shimizu, “Stiffness Control of Tendon Driven Multi-DOF Joint by Actuator with Non Linear Elastic System (ANLES),” J. of the Robotics Society of Japan, Vol.22, Issue 8, pp. 1043-1049, 2004. https://doi.org/10.7210/jrsj.22.1043
- [6] T. Kozuki, H. Mizoguchi, Y. Asano, M. Osada, T. Shirai, J. Urata, Y. Nakanishi, K. Okada, and M. Inaba, “Design Methodology for the Thorax and Shoulder of Human Mimetic Musculoskeletal Humanoid Kenshiro—A Thorax with Rib like Surface—,” Proc. IEEE/RSJ Int. Conf. Intell. Robot. Syst., pp. 4367-4372, 2012. https://doi.org/10.1109/IROS.2012.6386166
- [7] H. Dong, N. Figueroa, and A. El Saddik, “Adaptive “load-distributed” muscle coordination method for kinematically redundant musculoskeletal humanoid systems,” Robotics and Autonomous Systems, Vol.64, pp. 59-69, 2015. https://doi.org/10.1016/j.robot.2014.10.020
- [8] H. Ryu, Y. Nakata, Y. Okadome, Y. Nakamura, and H. Ishiguro, “Study on a Pneumatically Actuated Robot for Simulating Evolutionary Developmental Process of Musculoskeletal Structures,” J. Robot. Mechatron., Vol.28, No.2, pp. 226-233, 2016. https://doi.org/10.20965/jrm.2016.p0226
- [9] A. G. Feldman, “Once More on the Equilibrium-Point Hypothesis (λ Model) for Motor Control,” Motor Behavior, Vol.18, Issue 1, pp. 17-54, 1986. https://doi.org/10.1080/00222895.1986.10735369
- [10] N. Hogan, “An organizing principle for a class of voluntary movements,” J. Neuroscience, Vol.4, No.11, pp. 2745-2754, 1984. https://doi.org/10.1523/JNEUROSCI.04-11-02745.1984
- [11] M. Kawato, K. Furukawa, and R. Suzuki, “A Hierarchical Neural-Network Model for Control and Learning of Voluntary Movement,” Biol. Cybern., Vol.57, pp. 169-185, 1987. https://doi.org/10.1007/BF00364149
- [12] M. L. Latash, “Neurophysiological Basis of Movement,” Human Kinetics, 1998.
- [13] N. Bernstein, “Chapter II The Problem of the Interrelation of Co-Ordination and Localization,” Advances in Psychology, Vol.17, pp. 77-119, 1984. https://doi.org/10.1016/S0166-4115(08)61370-9
- [14] E. P. Loeb, S. F. Giszter, P. Saltiel, E. Bizzi, and F. A. Mussa-Ivaldi, “Output units of motor behavior: An experimental and modeling study,” J. of Cognitive Neuroscience, Vol.12, Issue 1, pp. 78-97, 2000. https://doi.org/10.1162/08989290051137611
- [15] E. Watanabe, H. Hirai, and H. I. Krebs, “Equilibrium Point-based Control of Muscle-driven Anthropomorphic Legs Reveals Modularity of Human Motor Control during Pedalling,” Advanced Robotics, Vol.34, Issue 5, pp. 328-342, 2020. https://doi.org/10.1080/01691864.2019.1708790
- [16] M. Kasaki, H. Ishiguro, M. Asada, M. Osaka, and T. Fujikado (Eds.), “Cognitive Neuroscience Robotics A: Synthetic Approaches to Human Understanding,” Springer, 2016.
- [17] S. Nakamura, Y. Kobayashi, and T. Mastuura, “Grid-Based Estimation of Transformation Between Partial Relationships Using a Genetic Algorithm,” J. Robot. Mechatron., Vol.34, No.4, pp. 786-794, 2022. https://doi.org/10.20965/jrm.2022.p0786
- [18] H. Kino, S. Kikuchi, Y. Matsutani, K. Tahara, and T. Nishiyama, “Numerical analysis of feedforward position control for non-pulley-musculoskeletal system: A case study of muscular arrangements of a two-link planar system with six muscles,” Advanced Robotics, Vol.27, Issue 16, pp. 1235-1248, 2013. https://doi.org/10.1080/01691864.2013.824133
- [19] H. Kino, H. Ochi, Y. Matsutani, and K. Tahara, “Sensorless Point-to-point Control for a Musculoskeletal Tendon-driven Manipulator: Analysis of a Two-DOF Planar System with Six Tendons,” Advanced Robotics, Vol.31, Issue 16, pp. 851-864, 2017. https://doi.org/10.1080/01691864.2017.1372212
- [20] H. Ochi, H. Kino, K. Tahara, and Y. Matsutani, “Geometric conditions of a two-link-and-six muscle structure based on internal force stability,” ROBOMECH J., Vol.7, Article No.17, 2020. https://doi.org/10.1186/s40648-020-00164-3
- [21] H. Ochi, K. Komada, K. Tahara, and H. Kino, “Convergent Conditions of Feedforward Control for Musculoskeletal Systems with Multi 1-DOF Joints Driven by Monoarticular and Biarticular Muscles,” J. Robot. Mechatron., Vol.35, No.3, pp. 751-761, 2023. https://doi.org/10.20965/jrm.2023.p0751
- [22] M. Anđelić and C. M. da Fonseca, “Sufficient conditions for positive definiteness of tridiagonal matrices revisited,” Positivity, Vol.15, Issue 1, pp. 155-159, 2011. https://doi.org/10.1007/s11117-010-0047-y
- [23] C. R. Johnson, M. Neumann, and M. J. Tsatsomeros, “Conditions for the positivity of determinants,” Linear Multilinear Algebra, Vol.40, Issue 3, pp. 241-248, 1996. https://doi.org/10.1080/03081089608818442
- [24] S. Kawamura, H. Kino, and C. Won, “High Speed Manipulation by Using Parallel Wire Driven Robots,” Robotica, Vol.18, Issue 1, pp. 13-21, 2000. https://doi.org/10.1017/S0263574799002477
- [25] S. Arimoto, “Control Theory of Non-linear Mechanical Systems: A Passivity-based and Circuit-theoretic Approach,” Oxford University Press, 1996.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.