Paper:
Data-Driven Design of Fractional-Order PID Controllers: Optimization of Robust Servo-Regulator Performance
Kota Jinai*, Yusuke Tsunoda*
 , Natsuki Kawaguchi*, Orlando Arrieta**,***
, Natsuki Kawaguchi*, Orlando Arrieta**,***
 , and Takao Sato*
, and Takao Sato*

*Department of Mechanical Engineering, Graduate School of Engineering, University of Hyogo
2167 Shosha, Himeji, Hyogo 671-2280, Japan
**Instituto de Investigaciones en Ingeniería, Facultad de Ingeniería, Universidad de Costa Rica
San José 11501, Costa Rica
***Departament de Telecomunicació i d’Enginyeria de Sistemes, Universitat Autònoma de Barcelona
Bellaterra, Barcelona 08193, Spain
This study proposes a data-driven optimal robust design methodology for a fractional-order proportional-integral-derivative (FOPID) controller. This methodology concurrently determines the parameters of the FOPID controller and reference model under a stability-margin constraint by utilizing only one-shot input-output data. The stability margin, which is quantitatively defined as the maximum value of the sensitivity function, is specified by the designer. This approach ensures a balanced design based on the trade-off between robust stability and servo or regulator performance at a given robust-stability level. Numerical examples substantiate the superiority of the FOPID controller over the conventional integer-order proportional-integral-derivative controller.
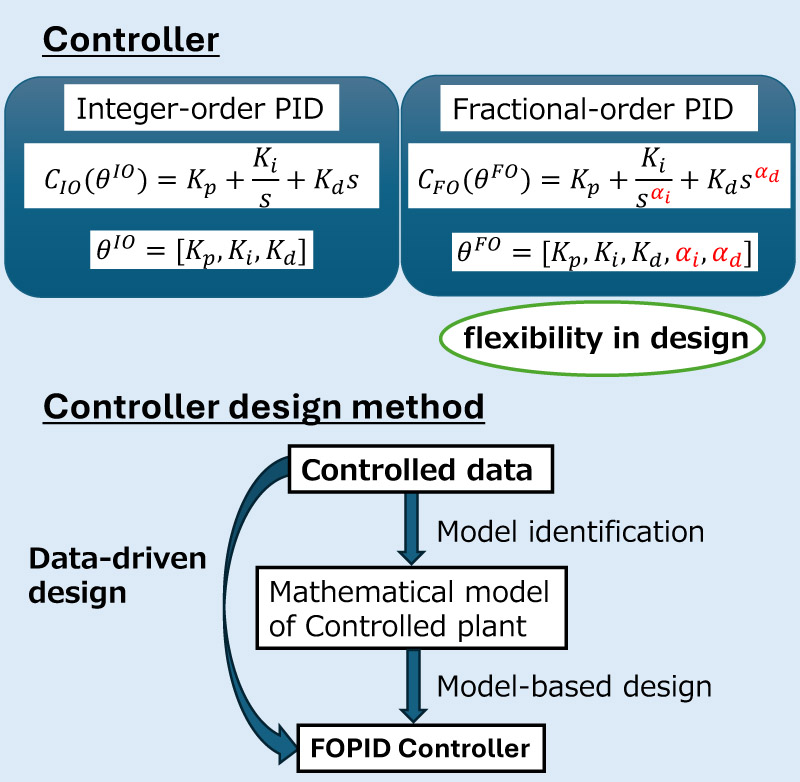
Data-driven design of Integer-order and fractional-order PID controllers
- [1] D. Soudbakhsh, A. M. Annaswamy, Y. Wang, S. L. Brunton, J. Gaudio, H. Hussain, D. Vrabie, J. Drgona, and D. Filev, “Data-Driven Control: Theory and Applications,” 2023 American Control Conf. (ACC), pp. 1922-1939, 2023. https://doi.org/10.23919/ACC55779.2023.10156081
- [2] F. Bruyne, “Iterative feedback tuning for internal model controllers,” Control Engineering Practice, Vol.11, No.9, pp. 1043-1048, 2003. https://doi.org/10.1016/S0967-0661(02)00237-X
- [3] H. Hjalmarsson, M. Gevers, S. Gunnarsson, and O. Lequin, “Iterative Feedback Tuning: Theory and Applications,” IEEE Control Systems, Vol.18, No.4, pp. 26-41, 1998. https://doi.org/10.1109/37.710876
- [4] S. Masuda, “PID controller tuning based on disturbance attenuation FRIT using one-shot experimental data due to a load change disturbance,” IFAC Proc. Volumes, Vol.45, No.3, pp. 92-97, 2012. https://doi.org/10.3182/20120328-3-IT-3014.00016
- [5] Y. Matsui, H. Ayano, S. Masuda, and K. Nakano, “Realization of Prefilter for Virtual Reference Feedback Tuning Using Closed-Loop Step Response Data,” J. Robot. Mechatron., Vol.28, No.5, pp. 707-714, 2016. https://doi.org/10.20965/jrm.2016.p0707
- [6] M. Nakamoto, “An application of the virtual reference feedback tuning for an MIMO process,” SICE 2004 Annual Conf., pp. 2208-2213, 2004. https://doi.org/10.11499/sicep.2004.0_26_3
- [7] M. Kano, K. Tasaka, M. Ogawa, A. Takinami, S. Takahashi, and S. Yoshii, “Extended fictitious reference iterative tuning and its application to chemical processes,” 2011 Int. Symp. on Advanced Control of Industrial Processes, pp. 379-384, 2011.
- [8] T. Sato and N. Kawaguchi, “Model-free design in a dual-rate system using finite impulse response filter,” Int. J. of Advanced Mechatronic Systems, Vol.11, No.1, pp. 1-10, 2024. https://doi.org/10.1504/IJAMECHS.2024.137564
- [9] Y. Sakai, N. Kawaguchi, and T. Sato, “Data-driven Response Estimation and Controller Tuning,” Trans. of the Institute of Systems, Control and Information Engineers, Vol.36, No.4, pp. 113-119, 2023. https://doi.org/10.5687/iscie.36.113
- [10] R. Vilanova and A. Visioli (Eds.), “PID Control in the Third Millennium,” Springer, 2012. https://doi.org/10.1007/978-1-4471-2425-2
- [11] A. O’Dwyer, “Handbook of PI and PID Controller Tuning Rules,” Imperial College Press, 2003. https://doi.org/10.1142/p575
- [12] H. Wu, W. Su, and Z. Liu, “PID controllers: Design and tuning methods,” 2014 9th IEEE Conf. on Industrial Electronics and Applications, pp. 808-813, 2014. https://doi.org/10.1109/ICIEA.2014.6931273
- [13] P. Aryan, G. L. Raja, R. Vilanova, and M. Meneses, “Repositioned Internal Model Control Strategy on Time-Delayed Industrial Processes with Inverse Behavior Using Equilibrium Optimizer,” IEEE Access, Vol.11, pp. 54556-54568, 2023. https://doi.org/10.1109/ACCESS.2023.3281691
- [14] V. M. Alfaro and R. Vilanova, “PID control: Resilience with respect to controller implementation,” Frontiers in Control Engineering, Vol.3, 2022. https://doi.org/10.3389/fcteg.2022.1061830
- [15] O. Arrieta, A. Barbieri, H. Meneses, F. Padula, R. Vilanova, and A. Visioli, “On the Use of Fractional-Order PID Controllers for TITO Processes,” IFAC-PapersOnLine, Vol.56, No.2, pp. 3284-3289, 2023. https://doi.org/10.1016/j.ifacol.2023.10.1470
- [16] D. Kumar, G. L. Raja, O. Arrieta, and R. Vilanova, “Fractional-order model identification and indirect internal model controller design for higher-order processes,” IFAC-PapersOnLine, Vol.56, No.2, pp. 7270-7275, 2023. https://doi.org/10.1016/j.ifacol.2023.10.337
- [17] J. Sabatier, “Modelling Fractional Behaviours Without Fractional Models,” Frontiers in Control Engineering, Vol.2, 2021. https://doi.org/10.3389/fcteg.2021.716110
- [18] A. Tepljakov, B. B. Alagoz, C. Yeroglu, E. A. Gonzalez, S. H. Hosseinnia, E. Petlenkov, A. Ates, and M. Cech, “Towards Industrialization of FOPID Controllers: A Survey on Milestones of Fractional-Order Control and Pathways for Future Developments,” IEEE Access, Vol.9, pp. 21016-21042, 2021. https://doi.org/10.1109/ACCESS.2021.3055117
- [19] A. Yonezawa, H. Yonezawa, S. Yahagi, and I. Kajiwara, “One-shot data-driven design of fractional-order PID controller considering closed-loop stability: Fictitious reference signal approach,” Vol.152, pp. 208-216, 2023. https://doi.org/10.1016/j.isatra.2024.07.001
- [20] F. Padula and A. Visioli, “Tuning rules for optimal PID and fractional-order PID controllers,” J. of Process Control, Vol.21, No.1, pp. 69-81, 2011. https://doi.org/10.1016/j.jprocont.2010.10.006
- [21] K. Jinai, N. Kawaguchi, O. Arrieta, and T. Sato, “Data-Driven Robust Servo Tuning Method Using Fractional-Order PID Controller,” IFAC-PapersOnLine, pp. 436-441, Vol.58, No.7, pp. 436-441, 2024. https://doi.org/10.1016/j.ifacol.2024.08.101
- [22] S. Masuda, X. Kong, K. Udagawa, and Y. Matsui, “Virtual reference feedback tuning using closed-loop step response data in frequency domain,” 2015 10th Asian Control Conf. (ASCC), 2015. https://doi.org/10.1109/ASCC.2015.7244763
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.