Top > JRM > Covariance Control for Uncrewed Aircraft Systems Under Correla ...

single-rb.php

JRM Vol.36 No.5 pp. 1082-1089
doi: 10.20965/jrm.2024.p1082
(2024)

Paper:

Views over last 60 days: 206

Covariance Control for Uncrewed Aircraft Systems Under Correlated Uncertainty

Yoshinori Matsuno ORCID Icon

Aviation Technology Directorate, Japan Aerospace Exploration Agency (JAXA)
6-13-1 Osawa, Mitaka, Tokyo 181-0015, Japan

Received:
March 19, 2024
Accepted:
August 19, 2024
Published:
October 20, 2024
Creative Commons License
Keywords:
convex programming, correlated uncertainty, covariance control, covariance steering, stochastic optimal control
Abstract

Uncrewed aircraft systems and advanced air mobility are associated with uncertain conditions, such as wind prediction errors, and they may deviate from dedicated airspaces referred to as corridors. However, further studies on these aspects are required. This study focuses on the covariance control for a stochastic discrete-time linear system under correlated uncertainties. A covariance control problem with chance constraints can be formulated as a convex-programming problem. Numerical simulations of uncrewed aircraft systems path planning can be used to compare two control laws: covariance control laws that consider correlated and noncorrelated noise. Numerical simulations were conducted to verify that the covariance control law considering correlated noise generates a trajectory that appropriately satisfies the constraints. Consequently, the effect of considering correlated noise in the covariance control law was clarified. In addition, covariance control has been demonstrated to generate appropriate trajectories for various state constraints. Moreover, numerical simulations indicated that covariance control facilitated the control of uncertainty, and the effectiveness of the covariance control was evaluated. The insights gained from the results of this study can inform enhanced uncertainty management for improving reliability and safety in real-world applications of uncrewed aircraft systems and advanced air mobility.

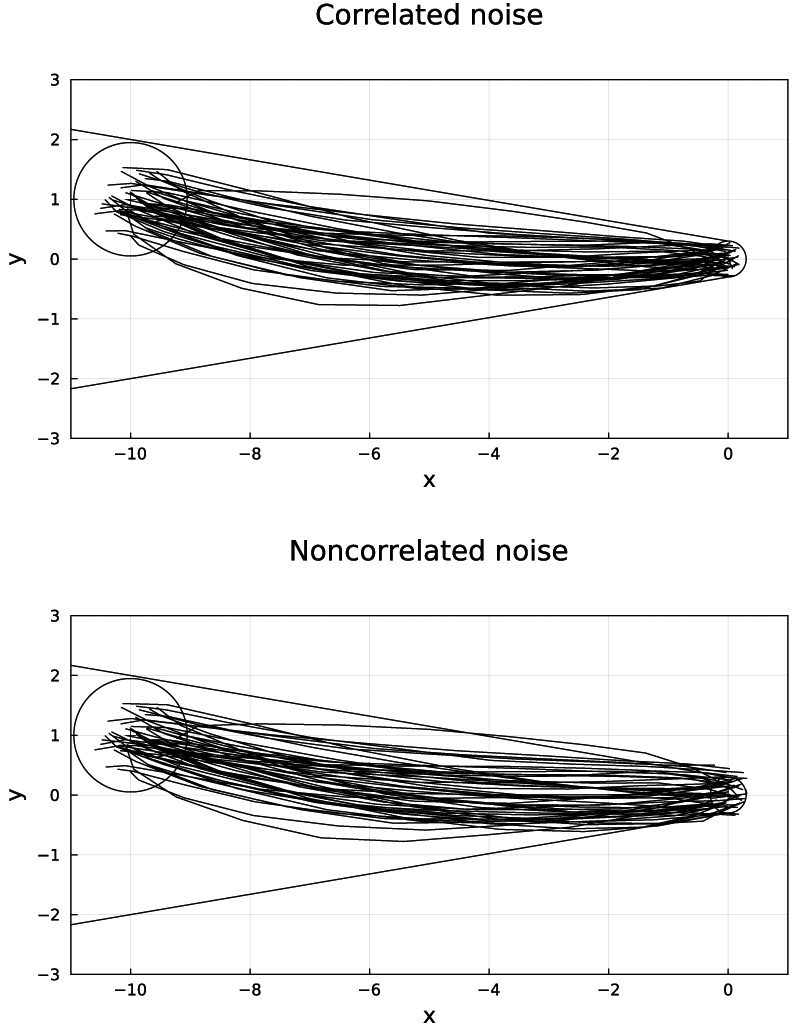
Covariance control results (Monte Carlo simulation with 50 trials)

Covariance control results (Monte Carlo simulation with 50 trials)

Cite this article as:
Y. Matsuno, “Covariance Control for Uncrewed Aircraft Systems Under Correlated Uncertainty,” J. Robot. Mechatron., Vol.36 No.5, pp. 1082-1089, 2024.
Data files:
References
  1. [1] M. S. Francis, “Unmanned air systems: Challenge and opportunity,” J. Aircr., Vol.49, pp. 1652-1665, 2012. https://doi.org/10.2514/1.C031425
  2. [2] H. Shakhatreh, A. H. Sawalmeh, A. Al-Fuqaha, Z. Dou, E. Almaita, I. Khalil, N. S. Othman, A. Khreishah, and M. Guizani, “Unmanned aerial vehicles (UAVs): A survey on civil applications and key research challenges,” IEEE Access, Vol.7, pp. 48572-48634, 2019. https://doi.org/10.1109/ACCESS.2019.2909530
  3. [3] R. Merkert and J. Bushell, “Managing the drone revolution: A systematic literature review into the current use of airborne drones and future strategic directions for their effective control,” J. Air Transp. Manag., Vol.89, Article No.101929, 2020. https://doi.org/10.1016/j.jairtraman.2020.101929
  4. [4] A. Goodchild and J. Toy, “Delivery by drone: An evaluation of unmanned aerial vehicle technology in reducing CO2,” Transp. Res. Part D: Transp. Environ., Vol.61, Part A, pp. 58-67, 2018. https://doi.org/10.1016/j.trd.2017.02.017
  5. [5] A. Oosedo, H. Hattori, I. Yasui, and K. Harada, “Unmanned aircraft system traffic management (UTM) simulation of drone delivery models in 2030 Japan,” J. Robot. Mechatron., Vol.33, No.2, pp. 348-362, 2021. https://doi.org/10.20965/jrm.2021.p0348
  6. [6] A. Straubinger, R. Rothfeld, M. Shamiyeh, K.-D. Büchter, J. Kaiser, and K. O. Plötner, “An overview of current research and developments in urban air mobility—Setting the scene for UAM introduction,” J. Air Transp. Manag., Vol.87, Article No.101852, 2020. https://doi.org/10.1016/j.jairtraman.2020.101852
  7. [7] L. A. Garrow, B. J. German, and C. E. Leonard, “Urban air mobility: A comprehensive review and comparative analysis with autonomous and electric ground transportation for informing future research,” Transp. Res. Part C: Emerg. Technol., Vol.132, Article No.103377, 2021. https://doi.org/10.1016/j.trc.2021.103377
  8. [8] Public-Private Committee for Advanced Air Mobility, “Concept of Operations for Advanced Air Mobility (ConOps for AAM),” 2023.
  9. [9] S. M. LaValle, “Planning algorithms,” Cambridge University Press, 2006.
  10. [10] B. Luders, M. Kothari, and J. How, “Chance constrained RRT for probabilistic robustness to environmental uncertainty,” AIAA Guidance, Navigation, and Control Conf., 2010. https://doi.org/10.2514/6.2010-8160
  11. [11] G. S. Aoude, B. D. Luders, J. M. Joseph, N. Roy, and J. P. How, “Probabilistically safe motion planning to avoid dynamic obstacles with uncertain motion patterns,” Auton. Robot., Vol.35, pp. 51-76, 2013. https://doi.org/10.1007/s10514-013-9334-3
  12. [12] L. Blackmore, M. Ono, and B. C. Williams, “Chance-constrained optimal path planning with obstacles,” IEEE Trans. Robot., Vol.27, Issue 6, pp. 1080-1094, 2011. https://doi.org/10.1109/TRO.2011.2161160
  13. [13] S. Satoh, H. Saijo, and K. Yamada, “Optimal position and attitude control of quadcopter using stochastic differential dynamic programming with input saturation constraints,” J. Robot. Mechatron., Vol.33, No.2, pp. 283-291, 2021. https://doi.org/10.20965/jrm.2021.p0283
  14. [14] K. Okamoto, M. Goldshtein, and P. Tsiotras, “Optimal covariance control for stochastic systems under chance constraints,” IEEE Control Syst. Lett., Vol.2, Issue 2, pp. 266-271, 2018. https://doi.org/10.1109/LCSYS.2018.2826038
  15. [15] K. Okamoto and P. Tsiotras, “Optimal stochastic vehicle path planning using covariance steering,” IEEE Robot. Autom. Lett., Vol.4, Issue 3, pp. 2276-2281, 2019. https://doi.org/10.1109/LRA.2019.2901546
  16. [16] E. Bakolas, “Optimal covariance control for discrete-time stochastic linear systems subject to constraints,” IEEE 55th Conf. on Decision and Control, pp. 1153-1158, 2016. https://doi.org/10.1109/CDC.2016.7798422
  17. [17] E. Bakolas, “Finite-horizon covariance control for discrete-time stochastic linear systems subject to input constraints,” Automatica, Vol.91, pp. 61-68, 2018. https://doi.org/10.1016/j.automatica.2018.01.029
  18. [18] R. Cole, C. Richard, S. Kim, and D. Bailey, “Assessment of the 60 km rapid update cycle (RUC) with near real-time aircraft reports,” Project Report NASA/A-1, 1998.
  19. [19] G. Chaloulos and J. Lygeros, “Effect of wind correlation on aircraft conflict probability,” J. Guid. Control Dyn., Vol.30, No.6, pp. 1742-1752, 2007. https://doi.org/10.2514/1.28858
  20. [20] B. O’Donoghue, E. Chu, N. Parikh, and S. Boyd, “Conic optimization via operator splitting and homogeneous self-dual embedding,” J. Optim. Theory Appl., Vol.169, pp. 1042-1068, 2016. https://doi.org/10.1007/s10957-016-0892-3
  21. [21] L. Blackmore and M. Ono, “Convex chance constrained predictive control without sampling,” AIAA Guid., Nav. and Control Conf., 2009. https://doi.org/10.2514/6.2009-5876
  22. [22] D. Mellinger and V. Kumar, “Minimum snap trajectory generation and control for quadrotors,” 2011 IEEE Int. Conf. Robot. Autom., pp. 2520-2525, 2011. https://doi.org/10.1109/ICRA.2011.5980409
  23. [23] Y. Mao, M. Szmuk, and B. Açıkmeşe, “Successive convexification of non-convex optimal control problems and its convergence properties,” IEEE 55th Conf. on Decis. Control, pp. 3636-3641, 2016. https://doi.org/10.1109/CDC.2016.7798816

Creative Commons License  This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.

*This site is desgined based on HTML5 and CSS3 for modern browsers, e.g. Chrome, Firefox, Safari, Edge, Opera.

Last updated on Mar. 19, 2025