Paper:
Development of a Curling Stone Delivery Robot with High Delivery Reproducibility
Tadaaki Sone
 and Takashi Kawamura
and Takashi Kawamura

Graduate School of Medicine, Science and Technology, Shinshu University
3-15-1 Tokida, Ueda, Nagano 386-8567, Japan
Curling is a two-player, zero-sum, finite, complete-information, uncertain game in which stones are delivered to a point approximately 37 m (120 ft). Despite its popularity, the dynamics of curling stones are unclear, and significant variations exist in the conditions of curling stones and curling sheets. It is essential to have a highly reproducible delivery apparatus that can perform tests in various environments to clarify stone dynamics and evaluate curling stones and sheets more accurately. In this study, we developed a delivery robot capable of delivering stones as quickly and accurately as, if not better than, a human using a large-diameter pneumatic cylinder. The delivery robot could deliver stones with high repeatability at 2.0 to 4.0 m/s by controlling the velocity of the pneumatic cylinder using multiple solenoid valves. In addition, we verified the accuracy of the robot’s velocity meter using motion capture to ensure that the throwing velocity measured by the delivery robot was sufficiently accurate. Finally, we conducted repeated delivery experiments using the delivery robot and demonstrated that the robot could deliver stones with high repeatability.
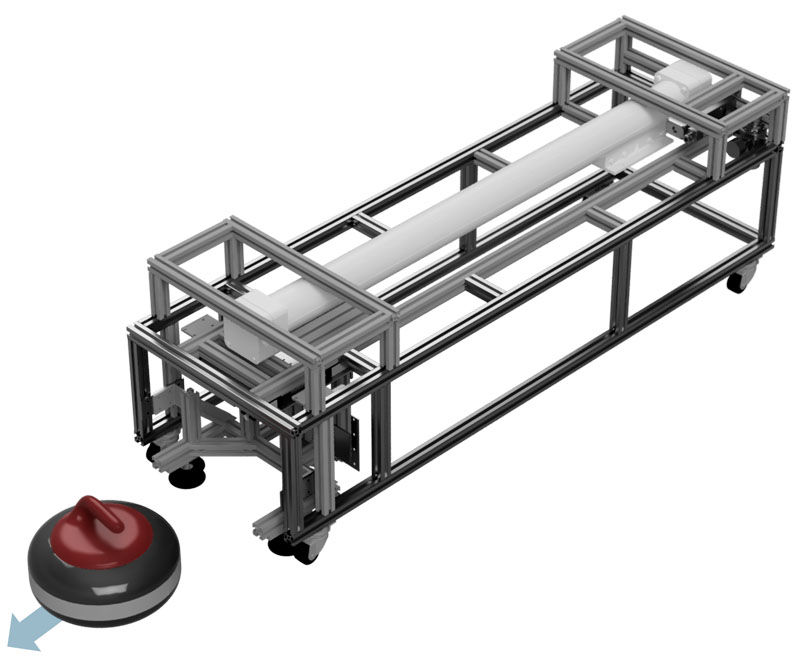
Delivery robot for curling stones by pneumatic
- [1] W. H. Macaulay and G. E. Smith, “Curling,” Nature, Vol.127, No.3193, p. 60, 1931. https://doi.org/10.1038/127060a0
- [2] G. Walker, “Mechanics of sport,” Nature, Vol.140, No.3544, pp. 567-568, 1937. https://doi.org/10.1038/140567a0
- [3] G. W. Johnston, “The dynamics of a curling stone,” Canadian Aeronautics and Space J., Vol.27, No.2, pp. 144-161, 1981.
- [4] M. R. A. Shegelski, R. Niebergall, and M. A. Walton, “The motion of a curling rock,” Canadian J. of Physics, Vol.74, Nos.9-10, pp. 663-670, 1996. https://doi.org/10.1139/p96-095
- [5] H. Nyberg, S. Alfredson, S. Hogmark, and S. Jacobson, “The asymmetrical friction mechanism that puts the curl in the curling stone,” Wear, Vol.301, Nos.1-2, pp. 583-589, 2013. https://doi.org/10.1016/j.wear.2013.01.051
- [6] M. R. A. Shegelski and E. Lozowski, “First principles pivot-slide model of the motion of a curling rock: Qualitative and quantitative predictions,” Cold Regions Science and Technology, Vol.146, pp. 182-186, 2018. https://doi.org/10.1016/j.coldregions.2017.10.021
- [7] J. Murata, “Study of curling mechanism by precision kinematic measurements of curling stone’s motion,” Scientific Reports, Vol.12, Article No.15047, 2022. https://doi.org/10.1038/s41598-022-19303-4
- [8] T. Kawamura, Y. Takegawa, and M. Yamamoto, “Scientific approach and challenges of curling study,” IEEJ Trans. on Electronics, Information and Systems, Vol.137, No.9, pp. 1137-1140, 2017 (in Japanese). https://doi.org/10.1541/ieejeiss.137.1137
- [9] K. Hoshino and W. D. G. Krishantha, “Control of air cylinder actuator with common bias pressure,” J. Robot. Mechatron., Vol.23, No.6, pp. 991-998, 2011. https://doi.org/10.20965/jrm.2011.p0991
- [10] Y. Sugimoto, K. Naniwa, D. Nakanishi, and K. Osuka, “Tension control of a McKibben pneumatic actuator using a dynamic quantizer,” J. Robot. Mechatron., Vol.35, No.4, pp. 1038-1046, 2023. https://doi.org/10.20965/jrm.2023.p1038
- [11] D. Sasaki, T. Noritsugu, M. Takaiwa, K. Nakanishi, and H. Maruta, “Development of wearable master-slave device for upper limb constructed with pneumatic rubber muscles,” J. of the Robotics Society of Japan, Vol.28, No.2, pp. 218-214, 2010. https://doi.org/10.7210/jrsj.28.208
- [12] K. G. Derpanis, “Overview of the RANSAC Algorithm,” Version 1.2, 2010.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.