Paper:
High-Speed Depth-Normal Measurement and Fusion Based on Multiband Sensing and Block Parallelization
Leo Miyashita*, Yohta Kimura*, Satoshi Tabata*, and Masatoshi Ishikawa*,**
*The University of Tokyo
7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8656, Japan
**Tokyo University of Science
1-3 Kagurazaka, Shinjuku-ku, Tokyo 162-8601, Japan
A wide range of research areas have high expectations for the technology to measure 3D shapes, and to reconstruct the shape of a target object in detail from multiple data. In this study, we consider a high-speed shape measurement technology that realizes accurate measurements in dynamic scenes in which the target object is in motion or deforms, or where the measurement system itself is moving. We propose a measurement method that sacrifices neither measurement density nor accuracy while realizing high speed. Many conventional 3D shape measurement systems employ only depth information to reconstruct a shape, which makes it difficult to capture the irregularities of an object’s surface in detail. Meanwhile, methods that measure the surface normal to capture 3D shapes can reconstruct high-frequency components, although low-frequency components tend to include integration errors. Thus, depth information and surface normal information have a complementary relationship in 3D shape measurements. This study proposes a novel optical system that simultaneously measures the depth and normal information at high speed by waveband separation, and a method that reconstructs the high-density, high-accuracy 3D shape at high speed from the two obtained data types by block division. This paper describes the proposed optical system and reconstruction method, and it evaluates the computation time and the accuracy of reconstruction using an actual measurement system. The results confirm that the high-speed measurement was conducted at 400 fps with pixel-wise measurement density, and a measurement accuracy with an average error of 1.61 mm.
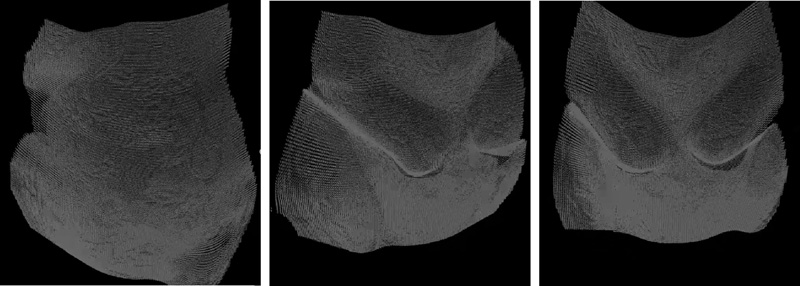
Results of depth-normal fusion
- [1] M. Ikura, L. Miyashita, and M. Ishikawa, “Stabilization System for UAV Landing on Rough Ground by Adaptive 3D Sensing and High-Speed Landing Gear Adjustment,” J. Robot. Mechatron., Vol.33, No.1, pp. 108-118, 2021.
- [2] J. Chen, Q. Gu, T. Aoyama, T. Takaki, and I. Ishii, “Blink-Spot Projection Method for Fast Three-Dimensional Shape Measurement,” J. Robot. Mechatron., Vol.27, No.4, pp. 430-443, 2015.
- [3] A. Obara, X. Yang, and H. Oku, “Structured Light Field Generated by Two Projectors for High-Speed Three Dimensional Measurement,” J. Robot. Mechatron., Vol.28, No.4, pp. 523-532, 2016.
- [4] H. Gao, H. T. Takaki, and T. Ishii, “GPU-based real-time structured light 3D scanner at 500 fps,” Proc. of Real-Time Image and Video Processing, Int. Society for Optics and Photonics (SPIE), Vol.8437, pp. 194-202, 2012.
- [5] Y. Watanabe, T. Komuro, and M. Ishikawa, “955-fps real-time shape measurement of a moving/deforming object using high-speed vision for numerous-point analysis,” Proc. of IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 3192-3197, 2007.
- [6] S. Tabata, S. Noguchi, Y. Watanabe, and M. Ishikawa, “High-speed 3D sensing with three-view geometry using a segmented pattern,” Proc. of IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), pp. 3900-3907, 2015.
- [7] R. J. Woodham, “Photometric Method For Determining Surface Orientation From Multiple Images,” Optical Engineering, Vol.19, No.1, 1980.
- [8] C. Hernandez, G. Vogiatzis, G. J. Brostow, B. Stenger, and R. Cipolla, “Non-rigid Photometric Stereo with Colored Lights,” Proc. of IEEE Int. Conf. on Computer Vision (ICCV), pp. 1-8, 2007.
- [9] R. J. Woodham, “Gradient and curvature from the photometric-stereo method, including local confidence estimation,” J. of the Optical Society of America, Vol.11, pp. 3050-3068, 1994.
- [10] L. Miyashita, Y. Watanabe, and M. Ishikawa, “MIDAS Projection: Markerless and Modelless Dynamic Projection Mapping for Material Representation,” ACM Trans. on Graphics, Vol.37, No.6, pp. 196:1-196:12, 2018.
- [11] L. Miyashita, A. Nakamura, T. Odagawa, and M. Ishikawa, “BIFNOM: Binary-Coded Features on Normal Maps,” Sensors, Vol.21, No.10, Article No.3469, 2021.
- [12] D. Nehab, S. Rusinkiewicz, J. Davis, and R. Ramamoorthi, “Efficiently combining positions and normals for precise 3D geometry,” ACM Trans. on Graphics, Vol.24, No.3, pp. 536-543, 2005.
- [13] L. Miyashita, Y. Kimura, S. Tabata, and M. Ishikawa, “High-speed simultaneous measurement of depth and normal for real-time 3D reconstruction,” Proc. of SPIE Optical Engineering + Applications, 11842-52, 2021.
- [14] W. Jang, C. Je, Y. Seo, and S. W. Lee, “Structured-light stereo: Comparative analysis and integration of structured-light and active stereo for measuring dynamic shape,” Optics and Lasers in Engineering, Vol.51, No.11, pp. 1255-1264, 2013.
- [15] B. K. P. Horn and M. J. Brooks, “The Variational Approach to Shape From Shading,” Computer Vision, Graphics, and Image Processing, Vol.33, No.2, pp. 174-208, 1986.
- [16] R. T. Frankot and R. Chellappa, “A Method for Enforcing Integrability in Shape from Shading Algorithms,” IEEE Trans. on Pattern Analysis and Machine Intelligence, Vol.10, No. 4, pp. 439-451, 1988.
- [17] J. D. Durou, J. F. Aujol, and F. Courteille, “Integration of a normal field in the presence of discontinuities,” Proc. of the 7th Int. Workshop on Energy Minimization Methods in Computer Vision and Pattern Recognition, Lecture Notes in Computer Science, Vol.5681, pp. 261-273, 2009.
- [18] M. Bähr, M. Breuß, Y. Quéau, A. S. Boroujerdi, and J. D. Durou, “Fast and accurate surface normal integration on non-rectangular domains,” Comput. Vis. Media 3, pp. 107-129, 2017.
- [19] A. Kerr, D. Campbell, and M. Richards, “QR decomposition on GPUs,” Proc. of 2nd Workshop on General Purpose Processing on Graphics Processing Units (GPGPU-2), Association for Computing Machinery, pp. 71-78, 2009.
- [20] G. Deng and L. W. Cahill, “An adaptive Gaussian filter for noise reduction and edge detection,” IEEE Conf. Record Nuclear Science Symposium and Medical Imaging Conf., Vol.3, pp. 1615-1619, 1993.
- [21] M. Kazhdan, M. Bolitho, and H. Hoppe, “Poisson Surface Reconstruction,” Proc. of Eurographics Symposium on Geometry Processing (SGP), pp. 61-70, 2006.
- [22] J. Vollmer, R. Mencl, and H. Mueller, “Improved Laplacian Smoothing of Noisy Surface Meshes,” Computer Graphics Forum, Vol.18, No.3, pp. 131-138, 1999.
- [23] G. Turk and M. Levoy, “Zippered Polygon Meshes from Range Images,” Proc. of the 21st Annual Conf. on Computer Graphics and Interactive Techniques (SIGGRAPH), pp. 311-318, 1994.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.