Paper:
Optimal Muscular Arrangement Using Genetic Algorithm for Musculoskeletal Potential Method with Muscle Viscosity
Hitoshi Kino*, Hiroaki Ochi**, and Kenji Tahara***
*Department of Mechanical and Systems Engineering, Chukyo University
101-2 Yagoto Honmachi, Showa-ku, Nagoya, Aichi 466-8666, Japan
**Department of Mechanical Engineering, Sanyo-Onoda City University
1-1-1 Daigakudori, Sanyo-Onoda-shi, Yamaguchi 756-0884, Japan
***Department of Mechanical Engineering, Kyushu University
744 Moto-oka, Nishi-ku, Fukuoka 819-0395, Japan
Muscle contractions (or equivalent mechanical elements) are responsible for joint movement in systems with musculoskeletal structure. Because muscles can only transmit force in the tensile direction in such systems, the internal force exists between the muscles. By utilizing the potential field generated by the internal force, the musculoskeletal potential method makes it possible to control the position without complex real-time calculations or sensory feedback by entering step-inputs of the balanced internal force at the target posture. However, the conditions of convergence to the target posture strongly depend on muscular arrangement. Previous studies have elucidated the mathematical conditions of the muscular arrangement; however, they provide sufficient conditions that must be satisfied by the muscular arrangement to converge to the target posture, which do not necessarily lead to optimal muscular arrangement conditions. This study proposes a method to determine the optimal muscular arrangement of a two-joint six-muscle system, wherein muscle viscosity is considered, that uses a genetic algorithm and an evaluation function considering the motion response time. The effect of the obtained muscular arrangement is verified in a simulation.
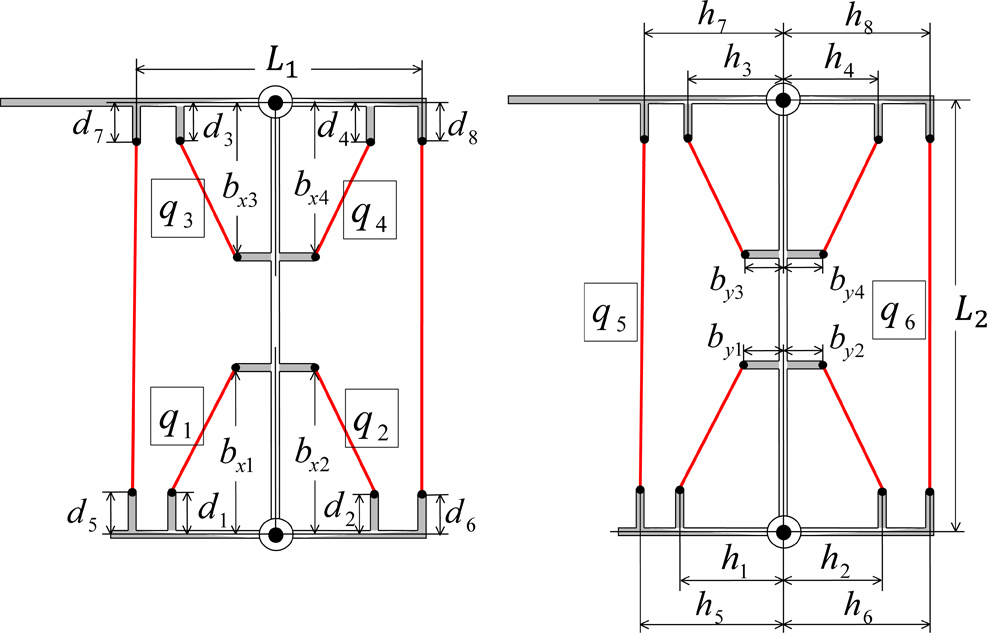
Parameters of muscular arrangement
- [1] H. Gomi and M. Kawato, “Human arm stiffness and equilibrium-point trajectory during multi-joint movement,” Biological Cybernetics, Vol.76, No.3, pp. 163-171, 1997.
- [2] M. Kumamoto, T. Oshima, and T. Yamamoto, “Control properties induced by the existence of antagonistic pairs of bi-articular muscles – mechanical engineering model analyses,” Human Movement Sci., Vol.13, No.5, pp. 611-634, 1994.
- [3] T. Oshima, K. Toriumi, T. Fujikawa, and N. Momose, “Effects of the Lower Leg Bi-Articular Muscle in Jumping,” J. Robot. Mechatron., Vol.16, No.6, pp. 643-648, 2004.
- [4] S. Hirose and S. Ma, “Redundancy decomposition control for multi-joint manipulator,” Proc. IEEE Int. Conf. on Robot. Automat., Scottsdale, AZ, pp. 119-124, 1989.
- [5] R. Ozawa, H. Kobayashi, and K. Hashirii, “Analysis, Classification, and Design of Tendon-Driven Mechanisms,” Trans. on Robot., Vol.30, No.2, pp. 396-410, 2014.
- [6] K. Koganezawa and Y. Shimizu, “Stiffness Control of Tendon Driven Multi-DOF Joint by Actuator with Non Linear Elastic System (ANLES),” Proc. Int. Conf. Robot. Autom., pp. 1184-1189, 2003.
- [7] T. Kozuki, H. Mizoguchi, Y. Asano, M. Osada, T. Shirai, J. Urata, Y. Nakanishi, K. Okada, and M. Inaba, “Design Methodology for Thorax and Shoulder of Human Mimetic Musculoskeletal Humanoid Kenshiro – A Thorax with Rib Like Surface –,” Proc. Int. Conf. Intell. Robot. Syst., pp. 4367-4372, 2012.
- [8] H. Endo and M. Wada, “A Musculo-skeletal Mechanism Simulating Human Forearm and Its Control Method,” J. Robot. Mechatron., Vol.5, No.3, pp. 248-252, 1993.
- [9] H. Ryu, Y. Nakata, Y. Okadome, Y. Nakamura, and H. Ishiguro, “Study on a Pneumatically Actuated Robot for Simulating Evolutionary Developmental Process of Musculoskeletal Structures,” J. Robot. Mechatron., Vol.28, No.2, pp. 226-233, 2016.
- [10] A. G. Feldman, “Once More on the Equilibrium-Point Hypothesis (λ Model) for Motor Control,” Motor Behavior, Vol.18, No.1, pp. 17-54, 1986.
- [11] N. Hogan, “An organizing principle for a class of voluntary movements, ” J. Neuroscience, Vol.4, No.11, pp. 2745-2754, 1984.
- [12] M. Kawato, K. Furukawa, and R. Suzuki, “A Hierarchical Neural-Network Model for Control and Learning of Voluntary Movement,” Biol. Cybern., Vol.57, pp. 169-185, 1982.
- [13] N. Bernstein, “Chapter II The problem of the Interrelation of Co-Ordination and Localization,” H. T. A. Whiting (Ed.), “Human Motor Actions: Bernstein Reassessed (Advances in Psychology),” pp. 77-119, Elsevier Science Ltd., 1984.
- [14] E. P. Loeb, S. F. Giszter, P. Saltiel, E. Bizzi, and F. A. Mussa-Ivaldi, “Output units of motor behavior: an experimental and modeling study,” J. Cognitive Neuroscience, Vol.12, No.1, pp. 78-97, 2000.
- [15] E. Watanabe, H. Hirai, and H. I. Krebs, “Equilibrium Point-based Control of Muscle-driven Anthropomorphic Legs Reveals Modularity of Human Motor Control during Pedalling,” Advanced Robotics, Vol.43, Issue 5, pp. 328-342, 2020.
- [16] M. Kasaki, H. Ishiguro, M. Asada et al. (Eds.), “Cognitive Neuroscience Robotics A: Synthetic Approaches to Human Understanding,” Springer, 2016.
- [17] H. Kino, S. Kikuchi, Y. Matsutani, K. Tahara, and T. Nishiyama, “Numerical Analysis of Feedforward Position Control for Non-pulley-musculoskeletal System: A case study of muscular arrangements of a two-link planar system with six muscles,” Advanced Robotics, Vol.27, No.16, pp. 1235-1248, 2013.
- [18] H. Kino, H. Ochi, Y. Matsutani, and K. Tahara, “Sensorless Point-to-point Control for a Musculoskeletal Tendon-Driven Manipulator: Analysis of a Two-DOF Planar System with Six Tendons,” Advanced Robotics, Vol.31, No.16, pp. 851-864, 2017.
- [19] H. Ochi, H. Kino, K. Tahara, and Y. Matsutani, “Geometric conditions of a two-link-and-six muscle structure based on internal force stability,” ROBOMECH J., Vol.7, 17, 2020.
- [20] Y. Matsutani, K. Tahara, H. Kino, and H. Ochi, “Complementary Compound Set-Point Control by Combining Muscular Internal Force Feedforward Control and Sensory Feedback Control Including a Time Delay,” Advanced Robotics, Vol.32, Issue 8, pp. 411-425, 2018.
- [21] T. Kosugi, H. Kino, and M. Goto, “Stability conditions of an ODE arising in human motion and its numerical simulation,” Results in Applied Mathematics, Vol.3, 100063, 2019,
- [22] Y. Matsutani, K. Tahara, and H. Kino, “Set-Point Control of a Musculoskeletal System Under Gravity by a Combination of Feed-Forward and Feedback Manners Considering Output Limitation of Muscular Forces,” J. Robot. Mechatron., Vol.31, No.4, pp. 612-620, 2019.
- [23] K. Tahara and H. Kino, “Reaching Movements of a Redundant Musculoskeletal Arm: Acquisition of an adequate internal force by iterative learning and its evaluation through a dynamic damping ellipsoid reaching movements of a redundant musculo-skeletal arm,” Advanced Robotics, Vol.24, Nos.5-6, pp. 783-818, 2010.
- [24] T. Okada, T. Imamura, T. Miyoshi, K. Terashima, Y. Yasuda, and T. Suzuki, “Muscle Strength Estimation Using Musculo-Skeletal Model for Upper Limb Rehabilitation,” J. Robot. Mechatron., Vol.20, No.6, pp. 863-871, 2008.
- [25] S. Kawamura, H. Kino, and C. Won, “High Speed Manipulation by Using Parallel Wire Driven Robots,” Int. J. of ROBOTICA, Vol.18, Part 1, pp. 13-21, 2000.
- [26] S. Arimoto, “Control theory of nonlinear mechanical systems: a passivity-based and circuit-theoretic approach,” Oxford University Press, 1996.
- [27] H. Mashima, K. Akazawa, H. Kushima, and K. Fujii, “The Force-load-velocity Relation and the Viscous-like Force in the Frog Skeletal Muscle,” Japanese J. of Physiology, Vol.22, Issue 1, pp. 103-120, 1972.
- [28] D. G. Thelen, “Adjustment of Muscle Mechanics Model Parameters to Simulate Dynamic Contractions in Older Adults,” J. Biomechanical Engineering, Vol.125, Issue 1, pp. 70-77, 2003.
- [29] D. E. Goldberg, “Genetic Algorithms in Search, Optimization, and Machine Learning,” Addison-Wesley Professional, 1989.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.