Paper:
Tracking Control of a Micro Ground Vehicle Using the Course Coordinate
Masanori Harada and Yuki Ueyama
National Defense Academy of Japan
1-10-20 Hashirimizu, Yokosuka, Kanagawa 239-8686, Japan
In this study, the tracking control of a micro ground vehicle (MGV) is investigated using the course coordinate. The course layout, which consists of the straight section and the curved section, is defined by the course coordinate with the station axis and the lateral position axis. The course angle and the curvature, which are defined as functions of the station value from the optimization technique, are used in the feedforward and feedback control of the tracking controller. The proposed method is evaluated using numerical simulations and indoor experiments. The results show that the MGV can successfully track the target lane and perform the double lane-change well.
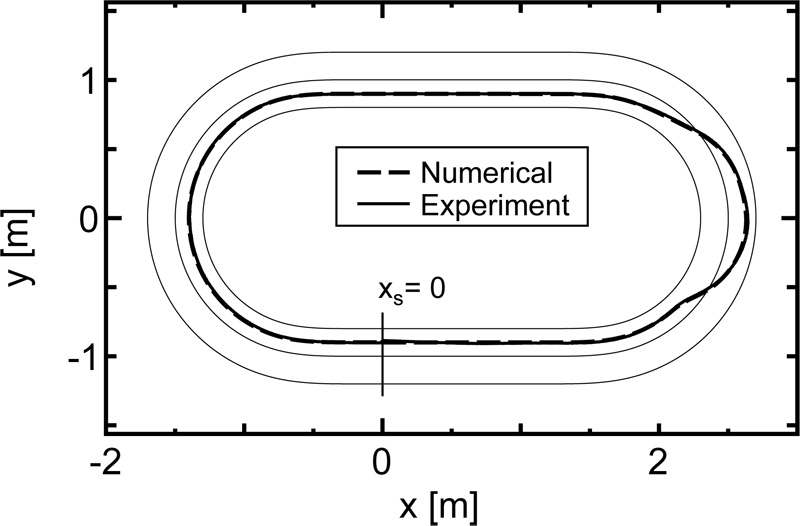
Double lane-change in the curved section
- [1] H. Yoshida, M. Omae, and T. Wada, “Toward Next Active Safety Technology of Intelligent Vehicle,” J. Robot. Mechatron., Vol.27, No.6, pp. 610-615, 2015.
- [2] S. Kato and S. Tsugawa, “Automated Lane Change Control of Vision-Based Vehicle,” J. Robot. Mechatron., Vol.13, No.4, pp. 395-401, 2001.
- [3] M. Hamaguchi and T. Taniguchi, “Emergency Avoidance Control System for an Automatic Vehicle – Slip Ratio Control Using Sliding Mode Control and Real-Time-Coded Immune Algorithm –,” J. Robot. Mechatron., Vol.27, No.6, pp. 645-652, 2015.
- [4] D. Yang, T. J. Gordon, M. Jonsson, and B. Jacobson, “Application of An Optimal Vehicle Path Controller on Curved Roads after Collisions,” Proc. of 12th Int. Symp. on Advanced Vehicle Control (AVEC2014), Mo-B1-2, 2014.
- [5] D. Casanova, R. S. Sharp, and P. Symonds, “Minimum Time Manoeuvring: The Significance of Yaw Inertia,” Vehicle System Dynamics, Vol.34, No.2, pp. 77-115, 2000.
- [6] J. Takahashi, H. Altmannshofer, M. Yamakado, and A. Zlocki, “A new longitudinal-motion assists control based on the combination of Adaptive Cruise Control and Preview G-Vectoring Control,” Proc. of 12th Int. Symp. on Advanced Vehicle Control (AVEC2014), Th-A2-2, 2014.
- [7] S. Watanabe and M. Harada, “Analysis of Optimal Maneuver Using an Obstacle Layout Method,” Trans. of Japan Society of Mechanical Engineers, Vol.80, No.817, pp. 1-12, 2014 (in Japanese).
- [8] Z. Ercan, A. Carvalho, S. Lefévre, F. Borrelli, H. E. Tseng, and M. Goksan, “Torque-Based Steering Assistance for Collision Avoidance During Lane Changes,” Proc. of 13th Int. Symp. on Advanced Vehicle Control (AVEC2016), Th-C3-2, 2016.
- [9] I. M. Ross and P. Sekhavat, “Optimal Feedback Control: Foundations, Examples, and Experimental Results for a New Approach,” J. of Guidance, Control, and Dynamics, Vol.31, No.2, pp. 307-321, 2008.
- [10] S. Watanabe and M. Harada, “Real-Time Optimal Obstacle Avoidance of MGV Using Modified Carathéodory-π Solutions,” Proc. of 13th Int. Symp. on Advanced Vehicle Control (AVEC2016), Th-A1-4, 2016.
- [11] M. Harada and Y. Ueyama, “Clock-Based Real-Time Optimal Control in Curved Road Section,” Trans. of Society of Automotive Engineers of Japan, Vol.50, No.6, pp. 1575-1580, 2019 (in Japanese).
- [12] S. Watanabe and M. Harada, “Optimal Tracking Control of an Micro Ground Vehicle,” J. Robot. Mechatron., Vol.27, No.6, pp. 653-659, 2015.
- [13] S. Watanabe and M. Harada, “Experimental Study on Optimal Tracking Control of an Micro Ground Vehicle,” J. Robot. Mechatron., Vol.29, No.4, pp. 757-765, 2017.
- [14] F. Lan, H. Tamai, and H. Makino, “Interpolation of Arbitrary Point Sequence by Triple Clothoid Curves,” J. of the Japan Society for Precision Engineering, Vol.76, No.10, pp. 1194-1199, 2010 (in Japanese).
- [15] S. Arita and P. Raksincharoensak, “A Path Planning Method with Specification of Curvatures of Boundary Conditions Based on Clothoid Curve Elements,” Trans. of Japan Society of Mechanical Engineers, Vol.85, No.878, pp. 1-15, 2019 (in Japanese).
- [16] A. E. Bryson and Y.-C. Ho, “Applied Optimal Control,” Taylor & Francis, 1975.
- [17] S. Ueno, “Minimum Fuel Cruise of Aircraft by Periodic Control,” J. of The Society of Instrument and Control Engineers, Vol.28, No.5, pp. 604-609, 1992 (in Japanese).
- [18] M. Harada, “Direct Trajectory Optimization by a Jacobi Pseudospectral Method with the Weights of High-Order Gauss-Lobatto Formulae,” Trans. of Japan Society of Mechanical Engineers, Series C, Vol.73, No.728, pp.119-124, 2007 (in Japanese).
- [19] H. Mouri and H. Furusho, “Investigation of Automatic Path Tracking – Control method for a curved path –,” Trans. of Society of Automotive Engineers of Japan, Vol.30, No.2, pp. 105-111, 1999 (in Japanese).
- [20] M. Harada, T. Nagatomo, Y. Mitani, and K. Yoshimoto, “Driver Model for a Vehicle Avoidance Maneuver in Cornering,” Trans. of Japan Society of Mechanical Engineers, Series C, Vol.72, No.720, pp. 2360-2365, 2006 (in Japanese).
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.