Paper:
High-Frequency Vibration of Leg Masses for Improving Gait Stability of Compass Walking on Slippery Downhill
Longchuan Li*, Fumihiko Asano*, and Isao Tokuda**
*School of Information Science, Japan Advanced Institute of Science and Technology
1-1 Asahidai, Nomi, Ishikawa 923-1292, Japan
**Department of Mechanical Engineering, Ritsumeikan University
1-1-1 Nojihigashi, Kusatsu, Shiga 825-8577, Japan
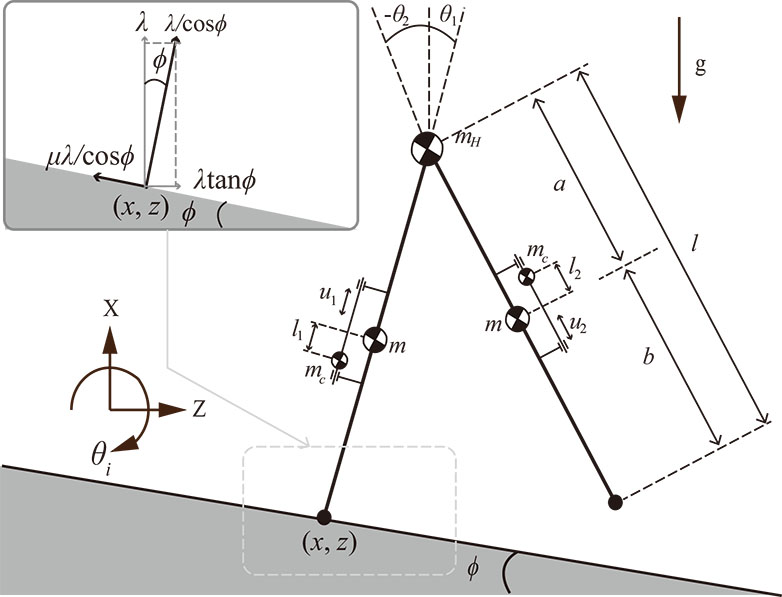
Towards improving the stability of point-foot biped robot on slippery downhill, a novel and indirect control method is introduced in this paper using active wobbling masses attached to both legs. The whole dynamics which contains walking, sliding and wobbling, can be dominated by high-frequency oscillation via entrainment effect. Stable gaits are therefore achieved by controlling only 1% of the whole system where the original passive dynamic walking fails. First, we derive the equations of dynamics and control for this indirectly controlled biped walking on slippery downhill. Second, we numerically show the possibility of improving the stability with high-frequency oscillation. We also find the main effect of wobbling motion on walking via phase-plane plot. Third, we prove that the range of stable walking with respect to frictional coefficient can be enlarged by employing suitable high-frequency oscillation via parametric study. Our method will be further applied to more general conditions in real tasks which contain different locomotion types, where the whole dynamics could be dominated by high-frequency oscillation and the phase properties of the dynamics will be positively utilized.
Motion stabilization with wobbling mass
- [1] T. McGeer, “Passive dynamic walking,” The Int. J. of Robotics Research, Vol.9, No.2, pp. 62-82, 1990.
- [2] T. Kinugasa and Y. Sugimoto, “Dynamically and Biologically Inspired Legged Locomotion: A Review,” J. Robot Mechatron., Vol.29, No.3, pp. 456-470, 2017.
- [3] A. Goswami, B. Espiau, and A. Keramane, “Limit cycles and their stability in a passive bipedal gait,” Proc. of IEEE Int. Conf. on Robotics and Automation (ICRA), Vol.1, pp. 246-251, Minneapolis, MN, April 1996.
- [4] F. Asano, Z.-W. Luo, and M. Yamakita, “Biped gait generation and control based on a unified property of passive dynamic walking,” IEEE Trans. on Robotics, Vol.21, No.4, pp. 754-762, 2005.
- [5] J. E. Pratt and G. A. Pratt, “Exploiting natural dynamics in the control of a planar bipedal walking robot,” Proc. of the 36th Annual Allerton Conf. on Communication, Control, and Computing, pp. 739-748, Monticello, USA, September 1998.
- [6] S. Kajita, K. Kaneko, K. Harada, F. Kanehiro, K. Fujiwara, and H. Hirukawa, “Biped walking on a low friction floor,” 2004 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), Vol.4, pp. 3546-3552, Sendai, Japan, September-October 2004.
- [7] F. Asano, T. Saka, and T. Fujimoto, “Passive dynamic walking of compass-like biped robot on slippery downhill,” 2015 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), pp. 4113-4118, Hamburg, Germany, 2015.
- [8] F. Asano and Y. Harata, “Sliding Passive Dynamic Walking of Compass-Like Biped Robot: Collision Modeling, Necessary Conditions, and Complexity,” J. Robot Mechatron., Vol.29, No.3, pp. 509-519, 2017.
- [9] K. Kaneko, K. Harada, F. Kanehiro, G. Miyamori, and K. Akachi, “Humanoid robot HRP-3,” 2008 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), pp. 2471-2478, Nice, France, September 2008.
- [10] K. Kaneko, F. Kanehiro, S. Kajita, M. Morisawa, K. Fujiwara, K. Harada, and H. Hirukawa, “Slip observer for walking on a low friction floor,” 2005 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), pp. 634-640, Edmonton, Canada, August 2005.
- [11] F. Asano and I. Tokuda, “Indirectly controlled limit cycle walking of combined rimless wheel based on entrainment to active wobbling mass,” Multibody System Dynamics, Vol.34, No.2, pp. 191-210, 2014.
- [12] L. Li, F. Asano, and I. Tokuda, “High-speed and energy-efficient locomotion of a seed-like underactuated robot on level surface by utilizing asymmetric wobbling effects,” 2017 IEEE Int. Conf. on Robotics and Biomimetics (ROBIO), pp. 1014-1019, Macau, China, December 2017.
- [13] L. Li, F. Asano, and I. Tokuda, “Nonlinear analysis of an indirectly controlled sliding locomotion robot,” 2018 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), pp. 1-9, Madrid, Spain, October 2018.
- [14] Y. Akutsu, F. Asano, and I. Tokuda, “Passive dynamic walking of compass-like biped robot with dynamic absorbers,” 2014 IEEE/RSJ Int. Conf. on Intelligent Robots and System, pp. 4855-4860, Chicago, USA, September 2014.
- [15] Y. Hanazawa, T. Hayashi, M. Yamakita, and F. Asano, “High-speed limit cycle walking for biped robots using active up-and-down motion control of wobbling mass,” 2013 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), pp. 3649-3654, Tokyo, Japan, November 2013.
- [16] Y. Ikemata, A. Sano, and H. Fujimoto, “A physical principle of gait generation and its stabilization derived from mechanism of fixed point,” Proc. 2006 Int. Conf. on Robotics and Automation (ICRA), pp. 836-841, Orlando, USA, May 2006.
- [17] T. Harada, H. Tanaka, M. J. Hankins, and I. Z. Kiss, “Optimal waveform for the entrainment of a weakly forced oscillator,” Physical Review Letters, Vol.105, No.8, 088301, 2010.
- [18] L. Li, I. Tokuda, and F. Asano, “Optimal input waveform for an indirectly controlled limit cycle walker,” 2018 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), pp. 7454-7459, Madrid, Spain, October 2018.
- [19] K. Taira and H. Nakao, “Phase-response analysis of synchronization for periodic flows,” J. of Fluid Mechanics, Vol.846, doi: 10.1017/jfm.2018.327, 2018.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.