Paper:
Set-Point Control of a Musculoskeletal System Under Gravity by a Combination of Feed-Forward and Feedback Manners Considering Output Limitation of Muscular Forces
Yuki Matsutani*, Kenji Tahara**, and Hitoshi Kino***
*Department of Robotics, Faculty of Engineering, Kindai University
1 Takaya Umenobe, Higashi-hiroshima, Hiroshima 739-2116, Japan
**Department of Mechanical Engineering, Kyushu University
744 Moto’oka, Nishi-ku, Fukuoka 819-0395, Japan
***Department of Intelligent Mechanical Engineering, Fukuoka Institute of Technology
3-30-1 Wajirohigashi, Higashi-ku, Fukuoka 811-0295, Japan
This paper proposes a new control method for musculoskeletal systems, which combines a feed-forward input with a feedback input, while considering an output limit. Our previous research proposed a set-point control that used a complementary combination of feedback using a time delay and a muscular internal force feed-forward; it achieved robust and rapid positioning with relatively low muscular contraction forces. However, in that control method, the range of motion of the musculoskeletal system was limited within a horizontal plane. In other words, that system did not consider the effect of gravity. The controller proposed in this paper can achieve the reaching movement of the musculoskeletal system without requiring accurate physical parameters under gravity. Moreover, the input of the proposed method can be prevented from becoming saturated with the output limit. This paper describes the design of the proposed controller and demonstrates the effectiveness of the proposed method based on the results of numerical simulations.
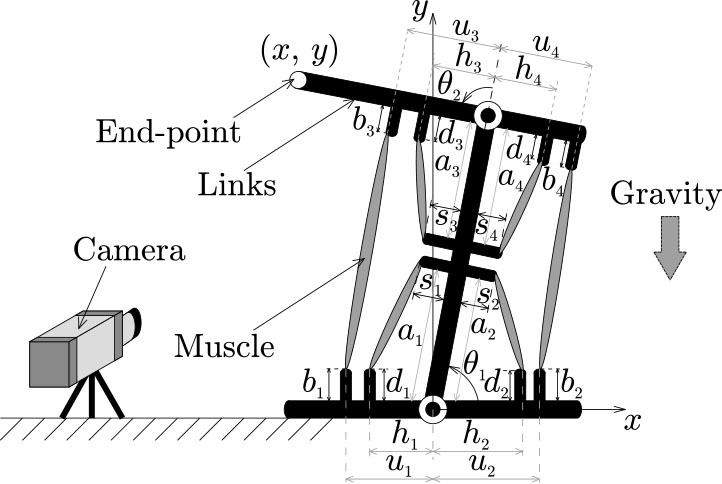
Musculoskeletal system
- [1] Y. Matsutani, K. Tahara, H. Kino, H. Ochi, and M. Yamamoto, “Set-point control of a musculoskeletal arm by the complementary combination of a feed-forward and feedback manner,” Proc. of the 2014 IEEE Int. Conf. on Robotics and Automation, pp. 5908-5914, 2014.
- [2] K. Tahara, Y, Matsutani, D. Nakagawa, M. Sato, and H. Kino, “Variable combination of feed-forward and feedback manners for set-point control of a musculoskeletal arm considering the maximum exertable muscular force,” Proc. of the 42nd Annual Conf. of the IEEE Industrial Electronics Society, pp. 815-820, 2016.
- [3] H. Kino, T. Yahiro, S. Taniguchi, and K. Tahara, “Sensorless position control using feedforward internal force for completely restrained parallel-wire-driven systems,” IEEE Trans. on Robotics, Vol.25, No.2, pp. 467-474, 2009.
- [4] H. Kino, S. Kikuchi, T. Yahiro, and K. Tahara, “Basic study of biarticular muscle’s effect on muscular internal force control based on physiological hypotheses,” Proc. of the 2009 IEEE Int. Conf. on Robotics and Automation, pp. 4195-4200, 2009.
- [5] H. Kino, S. Kikuchi, Y. Matsutani, K. Tahara, and T. Nishiyama, “Numerical analysis of feedforward position control for non-pulley musculoskeletal system: a case study of muscular arrangements of a two-link planar system with six muscles,” Advanced Robotics, Vol.27, No.16, pp. 1235-1248, 2013.
- [6] H. Kino, H. Ochi, Y. Matsutani, and K, Tahara, “Sensorless point-to-point control for a musculoskeletal tendon-driven manipulator: analysis of a two-DOF planar system with six tendons,” Advanced Robotics, Vol.31, No.16, pp. 851-864, 2017.
- [7] S. Arimoto, “Control theory of non-linear mechanical system: a passivity-based and circuit-theoretic approach,” Clarendon Press, 1996.
- [8] A. De Luca and S. Panzieri, “An iterative scheme for learning gravity compensation in flexible robot arms,” Automatica, Vol.30, No.6, pp. 993-1002, 1994.
- [9] A. Albu-Schaffer and G. Hirzinger, “A globally stable state feedback controller for flexible joint robots,” Advanced Robotics, Vol.15, No.8, pp. 799-814, 2001.
- [10] C. Ott, A. Albu-Schaffer, A. Kugi, S. Stramigioli, and G. Hirzinger, “A passivity based cartesian impedance controller for flexible joint robots – Part I: Torque feedback and gravity compensation,” Proc. of the 2004 IEEE Int. Conf. on Robotics and Automation, pp. 2659-2665, 2004.
- [11] A. De Luca, B. Siciliano, and L. Zollo, “PD control with on-line gravity compensation for robots with elastic joints: theory and experiments,” Automatica, Vol.41, No.10, pp. 1809-1819, 2005.
- [12] L. Zollo, B. Siciliano, A. De Luca, and E. Guglielmelli, “PD control with on-line gravity compensation for robots with flexible links,” Proc. of the 2007 European Control Conf., pp. 4365-4370, 2007.
- [13] K. Tahara, Z. W. Luo, S. Arimoto, and H. Kino, “Sensory-motor control mechanism for reaching movements of a redundant musculo-skeletal arm,” J. of Robotic Systems, Vol.22, No.11, pp. 639-651, 2005.
- [14] K. Tahara, Z. W. Luo, S. Arimoto, and H. Kino, “Sensory-motor control of a muscle redundant arm for reaching movements – Convergence analysis and gravity compensation,” Proc. 2005 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, pp. 1885-1891, 2005.
- [15] L. T. Dung, H. J. Kang, and Y. S. Ro, “Robot manipulator modeling in Matlab-Simmechanics with PD control and online gravity compensation,” Proc. of the IEEE Int. Forum on Strategic Technology 2010, pp. 446-449, 2010.
- [16] H. Zhang, M. Du, G. Wu, and W. Bu, “PD control with RBF neural network gravity compensation for manipulator,” Engineering Letters, Vol.26, No.2, pp. 236-244, 2018.
- [17] J. Huang, C. Yang, and J. Ye, “Nonlinear pd controllers with gravity compensation for robot manipulators,” Cybernetics and Information Technologies, Vol.14, No.1, pp. 141-150, 2014.
- [18] G. G. Muscolo, K. Hashimoto, A. Takanishi, and P. Dario, “A comparison between two force-position controllers with gravity compensation simulated on a humanoid arm,” J. of Robotics, doi:10.1155/2013/256364, 2013.
- [19] N. Ulrich and V. Kumar, “Passive mechanical gravity compensation for robot manipulators,” Proc. of the 1991 IEEE Int. Conf. on Robotics and Automation, pp. 1536-1541, 1991.
- [20] R. Altenburger, D. Scherly, and K. S. Stadler, “Design of a passive, iso-elastic upper limb exoskeleton for gravity compensation,” Robomech J., Vol.3, No.1, pp. 1-7, doi: 10.1186/s40648-016-0051-5, 2016.
- [21] K. Kaneda, H. Yamagata, and T. Morita, “Design method of spring balance mechanism through derivation of general solution,” J. Robot. Mechatron., Vol.31, No.2, pp. 305-316, 2019.
- [22] M. Ae, H. Tang, and T. Yokoi, “Estimation of inertia properties of the body segments in Japanese athletes,” Biomechanisms, Vol.11, pp. 23-33, 1992 (in Japanese).
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.