Paper:
Deformation Control of a Manipulator Based on the Zener Model
Taku Senoo, Kenichi Murakami, and Masatoshi Ishikawa
Graduate School of Information Science and Technology, The University of Tokyo
7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8656, Japan
In this study, passive dynamic control of a manipulator is designed and realized. According to the control strategy, the shift in the position and orientation of an end effector attributable to an external force is regarded as deformation of the robot. The Zener model, known as a standard linear solid model, is used to generate the deformable behavior, which describes the combination of plastic and elastic deformation. Based on the relation analysis between the Zener model and two other deformable models, two types of control methods are proposed in terms of the model’s expression. Physical simulations with a robotic arm are executed to validate the proposed control laws.
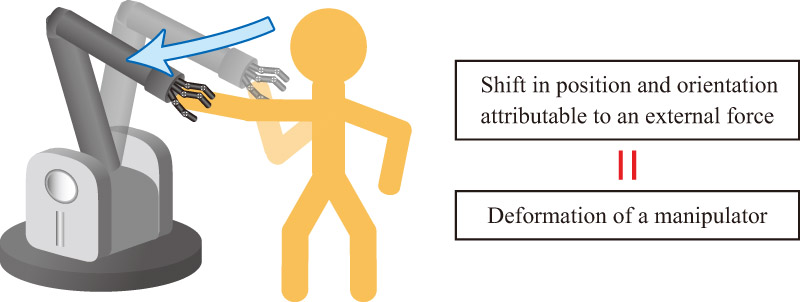
Concept of deformation control
- [1] S. Jien, S. Hirai, and K. Honda, “Miniaturization Design of Piezoelectric Vibration-Driven Pneumatic Unconstrained Valves,” J. Robot. Mechatron., Vol.22, No.1, pp. 91-99, 2010.
- [2] K. F. Laurin-Kovitz, J. E. Colgate, and S. D. R. Carnes, “Design of Components for Programmable Passive Impedance,” Proc. of IEEE Int. Conf. on Robotics and Automation, pp. 1476-1481, 1991.
- [3] C.-P. Chou and B. Hannaford, “Measurement and Modeling of McKibben Pneumatic Artificial Muscles,” IEEE Trans. on Robotics and Automation, Vol.12, No.1, pp. 90-102, 1996.
- [4] G. Zhang, J. Furusho, and M. Sakaguchi, “Vibration Suppression Control of Robot Arms Using a Homogeneous-Type Electrorheological Fluid,” IEEE/ASME Trans. on Mechatronics, Vol.5, No.3, pp. 302-309, 2000.
- [5] J. K. Salisbury, “Active Stiffness Control of a Manipulator in Cartesian Coordinates,” Proc. of IEEE Int. Conf. on Decision and Control, pp. 95-100, 1980.
- [6] M. Kaneko, K. Yokoi, and K. Tanie, “Direct Compliance Control for Serial Link Arm: 1st Report, Basic Concept and Decoupling Condition,” Trans. of the Japan Society of Mechanical Engineers, C, Vol.54, No.505, pp. 1510-1514, 1988.
- [7] N. Hogan, “Impedance Control: An Approach to Manipulation: Part I - Theory,” J. of Dynamic Systems, Measurement, and Control, Vol.107, No.1, pp. 1-7, 1985.
- [8] W.-S. Lu and Q.-H. Meng, “Impedance Control with Adaptation for Robotic Manipulations,” IEEE Trans. on Robotics and Automation, Vol.7, No.3, pp. 408-415, 1991.
- [9] A. Castano and S. Hutchinson, “Visual Compliance: Task-Directed Visual Servo Control,” IEEE Trans. on Robotics and Automation, Vol.10, No.3, pp. 334-342, 1994.
- [10] B. Siciliano, “Kinematic Control of Redundant Robot Manipulators: A Tutorial,” J. of Intelligent and Robotic Systems, Vol.3, No.3, pp. 201-212, 1990.
- [11] A. Albu-Schaffer, C. Ott, U. Frese, and G. Hirzinger, “Cartesian Impedance Control of Redundant Robots: Recent Results with the DLR-Light-Weight-Arms,” Proc. of IEEE Int. Conf. on Robotics and Automation, pp. 3704-3709, 2003.
- [12] H. Sadeghian, L. Villani, M. Keshmiri, and B. Siciliano, “Task-Space Control of Robot Manipulators with Null-Space Compliance,” IEEE Trans. on Robotics, Vol.30, No.2, pp. 493-506, 2014.
- [13] L. Zollo, B. Siciliano, A. De Luca, E. Guglielmelli, and P. Dario, “Compliance Control for a Robot with Elastic Joints,” Proc. of Int. Conf. on Advanced Robotics, pp. 1411-1416, 2003.
- [14] C. Ott, A. Albu-Schaffer, and G. Hirzinger, “Comparison of Adaptive and Nonadaptive Tracking Control Laws for a Flexible Joint Manipulator,” Proc. of IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, pp. 2018-2024, 2002.
- [15] B. Siciliano and W. J. Book, “A Singular Perturbation Approach to Control of Lightweight Flexible Manipulators,” Int. J. of Robotics Research, Vol.7, No.4, pp. 79-90, 1988.
- [16] G. Raiola, C. A. Cardenas, T. S. Tadele, T. de Vries, and S. Stramigioli, “Development of a Safety- and Energy-Aware Impedance Controller for Collaborative Robots,” IEEE Robotics and Automation Letters, Vol.3, No.2, pp. 1237-1244, 2018.
- [17] L. Peternel, N. Tsagarakis, and A. Ajoudani, “A Human-Robot Co-Manipulation Approach Based on Human Sensorimotor Information,” IEEE Trans. on Neural Systems and Rehabilitation Engineering, Vol.25, No.7, pp. 811-822, 2017.
- [18] H. Yu, S. Huang, G. Chen, Y. Pan, and Z. Guo, “Human-Robot Interaction Control of Rehabilitation Robots With Series Elastic Actuators,” IEEE Trans. on Robotics, Vol.31, No.5, pp. 1089-1100, 2015.
- [19] H. Modares, I. Ranatunga, S. Member, F. L. Lewis, and D. O. Popa, “Optimized Assistive Human-Robot Interaction Using Reinforcement Learning,” IEEE Trans. on Cybernetics, Vol.46, No.3, pp. 655-667, 2016.
- [20] A. Cherubini, R. Passamaa, A. Crosnier, A. Lasnier, and P. Fraisse, “Collaborative manufacturing with physical human-robot interaction,” Robotics and Computer-Integrated Manufacturing, Vol.40, pp. 1-13, 2016.
- [21] D. F. P. Granados, B. A. Yamamoto, H. Kamide, J. Kinugawa, and K. Kosuge, “Dance Teaching by a Robot: Combining Cognitive and Physical Human-Robot Interaction for Supporting the Skill Learning Process,” IEEE Robotics and Automation Letters, Vol.2, No.3, pp. 1452-1459, 2017.
- [22] T. Senoo, M. Koike, K. Murakami, and M. Ishikawa, “Visual Shock Absorber Based on Maxwell Model for Anti-Rebound Control,” Proc. of IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, pp. 1640-1645, 2015.
- [23] T. Senoo, M. Koike, K. Murakami, and M. Ishikawa, “Impedance Control Design Based on Plastic Deformation for a Robotic Arm,” IEEE Robotics and Automation Letters, Vol.2, No.1, pp. 209-216, 2017.
- [24] T. Senoo, G. Jinnai, K. Murakami, and M. Ishikawa, “Deformation Control of a Multijoint Manipulator Based on Maxwell and Voigt Models,” Proc. of IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, pp. 2711-2716, 2016.
- [25] T. Senoo, K. Murakami, and M. Ishikawa, “Deformable Robot Behavior Based on the Standard Linear Solid Model,” Proc. of IEEE Conf. on Control Technology and Applications, pp. 746-751, 2017.
- [26] A. Takacs, J. K. Tar, T. Haidegger, and I. J. Rudas, “Applicability of the Maxwell-Kelvin Model in Soft Tissue Parameter Estimation,” Proc. of Int. Symp. on Intelligent Systems and Informatics, pp. 115-119, 2014.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.