Paper:
Operator-Based Control System Analysis and Design for Nonlinear System with Input and Output Constraints
Shuhui Bi*, Lei Wang**, Shengjun Wen***, and Liyao Ma*
*School of Electrical Engineering, University of Jinan
No.336 West Road of Nanxinzhuang, Jinan, Shandong 250022, China
**HRG (Shandong) Intelligent Equipment Research Institute
No.1268 Gongye 4 Road, Jinan, Shandong 250000, China
***Zhongyuan University of Technology
No.41 Zhongyuan Load, Zhengzhou 450007, China
Smart material-based actuators and sensors have been widely used in practice owing to their various advantages. However, in the working process of these actuators and sensors, their output responses always deduce non-smooth nonlinear constraints. The constraint resulting from the actuator is called the input constraint and the constraint caused by the sensor is called the output constraint. These input and output constraints may induce inaccuracies and oscillations, severely degrading system performance. Therefore, the input and output constraints brought about by actuators and sensors should be considered in control system design. In this paper, system analysis for a nonlinear system with input and output constraints will be considered. The effect from the input constraint to the internal signal in the control system will be discussed. Moreover, the influence of the output constraint on the whole system will be studied. Further, the sufficient conditions for maintaining the stability of the system are obtained. Then, by using the robust right coprime factorization approach, an operator-based internal model like control structure is proposed for mitigating the input and output constraints. Finally, the effectiveness of the proposed design scheme will be confirmed through numerical simulation.
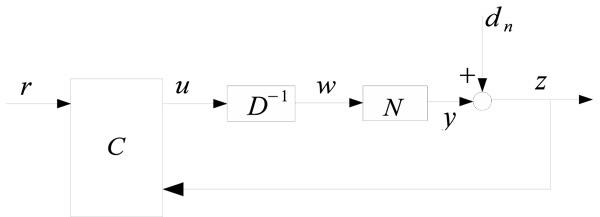
A nonlinear control system with output constraint
- [1] R. V. Iyer, X. Tan, and P. S. Krishnaprasad, “Approximate inversion of the Preisach hysteresis operator with application to control of smart actuators,” IEEE Trans. on Automatic Control, Vol.50, pp. 798-810, 2005.
- [2] M. A. Janaideh, S. Rakheja, and C. Y. Su, “An analytical generalized Prandtl-Ishlinskii model inversion for hysteresis compensation in micropositioning control,” IEEE Trans. on Mechatronics, Vol.16, No.4, pp. 734-744, 2011.
- [3] C. Y. Su, Y. Stepanenko, J. Svoboda, and T. P. Leungm, “Robust adaptive control of a class of nonlinear systems with unknown backlash-Like hysteresis,” IEEE Trans. on Automatic Control, Vol.45, No.12, pp. 2427-2432, 2000.
- [4] G. Tao and F. L. Lewis, “Adaptive control of nonsmooth dynamic systems,” Springer-Verlag, 2001.
- [5] S. Bi, L. Wang, and C. Han, “Robust control of nonlinear system with input and output nonlinear constraints,” J. Robot. Mechatron., Vol.29, No.6, pp. 1073-1081, 2017.
- [6] X. Tan and J. Baras, “Modeling and control of hysteresis in magnetostrictive actuators,” Automatica, Vol.40, No.9, pp. 1469-1480, 2004.
- [7] M. Brokate and J. Sprekels, “Hysteresis and phase transitions,” Springer-Verlag, 1996.
- [8] M. Ismail, F. Ikhouane, and J. Rodellar, “The hysteresis Bouc-Wen model, a survey,” Archives of Computational Methods in Engineering, Vol.16, No.2, pp. 161-188, 2009.
- [9] J. W. Macki, P. Nistri, and P. Zecca, “Mathematical models for hysteresis,” Soc. Indust. Appl. Math., Vol.35, pp. 94-123, 1993.
- [10] J. Oh and D. Bernstein, “Semilinear Duhem model for rate-independent and rate-dependent hysteresis,” IEEE Trans. on Automatic Control, Vol.50, No.5, pp. 631-645, 2005.
- [11] M. Rakotondrabe, “Bouc-Wen modeling and inverse multiplicative structure to compensate hysteresis nonlinearity in piezoelectric actuators,” IEEE Trans. Automat. Sci. Eng., Vol.8, No.2, pp. 428-431, 2001.
- [12] S. Bi, M. Deng, and S. Wen, “Operator-based output tracking control for nonlinear uncertain systems with unknown time-varying delays,” IET Control Theory and Applications, Vol.5, No.5, pp. 693-699, 2011.
- [13] S. Bi, M. Deng, and Y. Xiao, “Robust stability and tracking for operator-based nonlinear uncertain systems,” IEEE Trans. of Automation Science and Engineering, Vol.12, No.3, pp. 1059-1066, 2015.
- [14] S. Bi, L. Wang, Y. Zhao, and M. Deng, “Operator-based robust control for nonlinear uncertain systems with unknown Backlash-Like hysteresis,” Int. J. of Control, Automation and Systems, Vol.14, No.2, pp. 469-477, 2016.
- [15] M. Deng, A. Inoue, and Y. Baba, “Operator-based nonlinear vibration control system design of a flexible arm with Piezoelectric actuator,” Int. J. of Advanced Mechatronic Systems, Vol.1, No.1, pp. 71-76, 2008.
- [16] M. Deng, A. Inoue, and K. Ishikawa, “Operator-based nonlinear feedback control design using robust right coprime factorization,” IEEE Trans. on Automatic Control, Vol.51, No.4, pp. 645-648, 2006.
- [17] D. Wang, F. Li, S. Wen, X. Qi, P. Liu, and M. Deng, “Operator-based Sliding-Mode nonlinear control design for a process with input constraint,” J. Robot. Mechatron., Vol.27, No.1, pp. 83-90, 2015.
- [18] S. Bi, M. Deng, and A. Inoue, “Operator based internal model control of perturbed nonlinear systems,” Proc. of the 7th Asian Control Conf., Hong Kong, China, August 27-29, pp. 949-952, 2009.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.