Paper:
Designing a Communication Field with a Transformation Method
Xiangyang Lu*, Ling Ouyang*, Lijuan Sun*, Jin Hu**, and Lijuan Jia**
*School of Electronic and Information Engineering, Zhongyuan University of Technology
No.41 Zhongyuanzhong Road, Zhengzhou 450007, China
**School of Information and Electronics, Beijing Institute of Technology
5 Zhongguannan Road Haidian, Beijing 100081, China
The transformation method that was originally used to tailor the physical fields into desired spatial patterns by designing material parameters is used herein to obtain necessary local dynamic parameters when the state distribution of a network system is prescribed in space. This constitutes a typical inverse problem that controls the state distribution of a complex network by designing its local dynamic parameters. Thus, it is difficult to obtain a direct solution. This coordinate transformation provides a direct method. The feasibility of this method is demonstrated and verified by two examples (a communication field bender and a communication field cloak) in corresponding network systems.
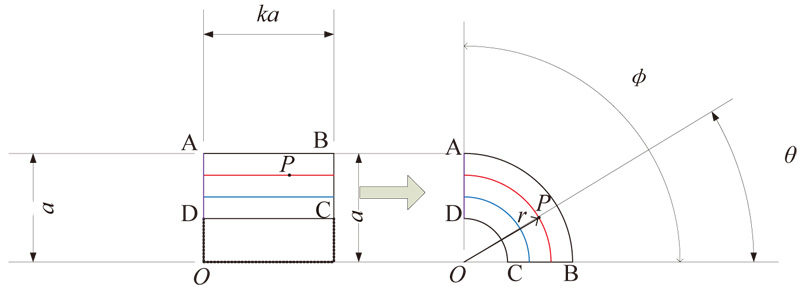
Transformation field bender
- [1] T. Gross and B. Blasius, “Adaptive coevolutionary networks: a review, ” J. of the Royal Society-Interface, Vol.5, pp. 259-27, 2008.
- [2] S. H. Strogatz, “Exploring the complex networks,” Nature Mar., pp. 268-276, 2001.
- [3] B. Yu and J. He, “Scale-free brain Scale-free brain activity: past, present and future,” Trends Cogn. Sci., Vol.18, pp. 480-487, 2014.
- [4] A. Tozzi, M. Zare, and A. A. Benasich, “New Perspectives on Spontaneous Brain Activity: Dynamic Networks and Energy Matter,” Front. Hum. Neurosci., Vol.10, No.247, 2016.
- [5] V. Afraimovich, I. Tristan, P. Varona, and M. Rabinovich, “Transient dynamics in complex systems: heteroclinic sequences with multidimensional unstable manifolds,” Int. J. Disc. Nonli. Complex, Vol.2, pp. 21-41, 2013.
- [6] M. Amft, D. Bzdok, A. R. Laird, P. T. Fox, L. Schilbach, and S. B. Eickhoff, “Definition and characterization of an extended social-affective default network,” Brain Struct. Funct., Vol.220, pp. 1031-1049, 2015.
- [7] G. W. Domhoff and K. C. Fox, “Dreaming and the default network: a review, synthesis and counterintuitive research proposal,” Conscious. Cogn., Vol.33C, pp. 342-353, 2015.
- [8] P. Barttfeld, L. Uhrig, J. D. Sitt, M. Sigman, B. Jarraya, and S. Dehaene, “Signature of consciousness in the dynamics of resting-state brain activity,” Proc. Natl. Acad. Sci. USA, Vol.112, pp. 887-892, 2015.
- [9] P. H. S. Michael and A. P. Mason, “Critical Truths About Power Laws,” Science, Vol.335, No.6069, pp. 665-666, 2012.
- [10] E. Okan, O. Mahmut, and Y. Nejat, “Impact of small-world topology on the performance of a feed-forward artificial neural network based on 2 different real-life problems,” Turk. J. Elec. Eng. and Comp. Sc., Vol.22, pp. 708-718, 2014.
- [11] D. J. Watts and S. H. Strogatz, “Collective dynamics of ‘small-world’ networks,” Nature, Vol.393, pp. 440-442, 1998.
- [12] A. L. Barabási, R. Albert, and H. Jeong, “Mean-field theory for scale-free random networks,” Physica A, Vol.272, p. 173, 1999.
- [13] Y. Naruoka, N. Hiramitsu, and Y. Mitsuya, “A Study of Power-Assist Technology to Reduce Body Burden During Loading and Unloading Operations by Support of Knee Joint Motion,” J. Robot. Mechatron., Vol.28, No.6, pp. 949-957, 2016.
- [14] M. Barahona and L. M. Pecora, “Synchronization in small world systems,” Phys. Rev. Lett., Vol.89, 054101, 2004.
- [15] I. V. Belykh, E. Lange, and M. Hasler, “Synchronization of bursting neurons:what matters in the network toplogoly,” Phys. Rev. Lett., Vol.94, 18801, 2005.
- [16] R. Criado, J. Flores, J. Pello, and M. Romance, “Optimal communication schemes in a complex network: From trees to bottleneck networks,” Eur. Phys. J. Special Topics, Vol.146, Issue 1, pp. 145-154, 2007.
- [17] X. Li, X. Wang, and G. Chen, “Pinning a complex dynamic network to its equilibrium,” IEEE Trans. on Circuits and Systems-I, Vol.51, pp. 2074-2087, 2004.
- [18] Y. Tang, Z. D. Wang, and J. A. Fang, “Pinning control of fractional-order weighted complex networks,” Chaos, Vol.19, 013112, 2009.
- [19] R. Guimera, A. D. Gulera, F. V. Redondo, and A. Cabrales, “Optimal network topologies for local search with congestion,” Phys. Rev. Lett., Vol.89, 248701, 2002.
- [20] H. Darweesh, E. Takeuchi, K. Takeda, Y. Ninomiya, A. Sujiwo, L. Morales, N. Akai, T. Tomizawa, and S. Kato, “Open Source Integrated Planner for Autonomous Navigation in Highly Dynamic Environments,” J. Robot. Mechatron., Vol.29, No.4, pp. 668-684, 2017.
- [21] Y. C. Zhang and M. Blattner, “Heat conduction process on community networks as a recommendation model,” Phys. Rev. Lett., Vol.99, 154301, 2007.
- [22] F. Schweitzer and J. A. Holyst, “Modelling collective opinion formation by means of active Brownian particles,” Eur. Phys. J. B, Vol.15, Issue 4, pp. 723-732, 2000.
- [23] I. Murasawa, S. Murofushi, C. Ishii, and H. Kawamura, “Development of a Robotic Laparoscope for Laparoscopic Surgery and its Control,” J. Robot. Mechatron., Vol.29, No.3, pp. 580-590, 2017.
- [24] C. Castellano, S. Fortunato, and V. Loreto, “Statistical physics of social dynamics,” Reviews of Modern Physics., Vol.81, No.2, pp. 591-646, 2009.
- [25] Y. Y. Liu, J. J. Slotine, and A. L. Barabási, “Controllability of complex networks,” Nature, Vol.437, pp. 167-173, 2011.
- [26] E. B. Lars, “Analysis of Direct Sensor-to-Embedded Systems Interfacing: A Comparison of Targets’ Performance,” Int. J. of Intelligent Mechatronics and Robotics, Vol.2, No.1, pp. 41-56, 2012.
- [27] N. Sarshar and V. Roychowdhury, “Scale-Free and Stable Structures in Complex Ad Hoc Networks,” Phys. Rev. E, Vol.69, 026101, 2004.
- [28] L. Marucci et al., “How to turn a genetic circuit into a synthetic tunable oscillator, or a bistable switch,” PLoS ONE, Vol.4, e8083, 2009.
- [29] J. Chen, J. Hu, X. B. Yang, and X. Y. Lu, “Manipulating and detecting the chirpiness of spatial chirp signals via fractional Fourier lenses designed by transformation optics,” Applied Optics, Vol.56, No.32, pp. 9119-9125, 2017.
- [30] M. Chiang, S. H. Low, A. R. Calderbank, and J. C. Doyle, “Layering as optimization decomposition: a mathematical theory of network architectures,” Proc. IEEE, Vol.95, pp. 255-312, 2007.
- [31] A. Greenleaf, M. Lassas, and G. Uhlmann, “On non-uniqueness for Calderón’s inverse problem,” Math. Res. Lett., Vol.10, No.5, pp. 685-693, 2003.
- [32] J. B. Pendry, D. Schurig, and D. R. Smith, “Controlling Electromagnetic Fields,” Science, Vol.312, Issue 5781, pp. 1780-1782, 2006.
- [33] U. Leonhardt, “Optical conformal mapping,” Science, Vol.312, pp. 1777-1780, 2006.
- [34] G. W. Milton, M. Briane, and J. R. Willis, “On cloaking for elasticity and physical equations with a transformation invariant form,” New J. Phys., Vol.8, p. 248, 2006.
- [35] Q. B. Deng, J. Hu, Z. Chang, X. M. Zhou, and G. K. Hu, “Theory and experiment of isotropic electromagnetic beam bender made of dielectric materials,” Advanced Materials Research, Vols.150-151, pp. 1508-1516, 2011.
- [36] Y. A. Urzhumov and D. S. Smith, “Fluid flow control with transformation media,” Phys. Rev. Lett., Vol.107, 074501, 2011.
- [37] J. Hu, X. M. Zhou, M. Hu, and G. K. Hu., “Nonsingular two dimensional cloak of arbitrary shape,” Appl. Phys. Lett., Vol.95, 011107, 2009.
- [38] J. Hu, X. M. Zhou, and G. K. Hu, “Design method for electromagnetic cloak with arbitrary shapes based on Laplace’s equation,” Opt. Express, Vol.17, Issue 3, pp. 1308-1320, 2009.
- [39] Y. Wang, T. Ran, and B. Z. Li, “Using the multi-living agent concept to investigate complex information systems,” Science in China Series F-Information, Vol.52, pp. 1-17, 2009.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.