Paper:
Design Method for Improvement of Transient-State Intersample Output of Multirate Systems Including Integrators
Tomonori Kamiya, Takao Sato, Nozomu Araki, and Yasuo Konishi
Graduate School of Engineering, University of Hyogo
2167 Shosha, Himeji, Hyogo 671-2280, Japan
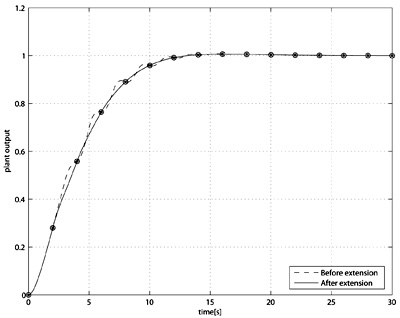
Comparison of output responses
- [1] M. Araki and T. Hagiwara, “Pole Assignment by Multirate Sampled-data Output Feedback,” Int. J. Control, Vol.44, No.6, pp. 1661-1673, 1986.
- [2] T. Chen and B. Francis, “Optimal Sampled-Data Control Systems,” Springer-Verlag, London, 1995.
- [3] A. Tangirala, D. Li, R. Patwardhan, S. Shah, and T. Chen, “Issues in Multirate Process Control,” Proc. of American Control Conf., pp. 2771-2775, 1999.
- [4] A. Inoue and M. Deng, “An optimal robust controller with multi-rate output feedback by using symbolic computation,” Proc. of the 2014 Int. Conf. on Advanced Mechatronic Systems, pp. 224-228, Luoyang, China, 2013.
- [5] H. Werner, “Generalized sampled-data hold functions for robust multivariable tracking and disturbance rejection,” Optimal Control Applications and Methods, Vol.22, pp. 75-93, 2001.
- [6] H. Fujioka and S. Hara, “Synthesis of sampled-data Hinfty servo controller with generalized hold,” Proc. of 42nd IEEE CDC, pp. 2302-2307, 2003.
- [7] T. Sato, “Parametric Design of Dual-Rate Controller for Improvement in Steady-State Intersample Response,” SICE J. of Control, Measurement, and System Integration, Vol.1, No.4, pp. 329-334, 2008.
- [8] B. M. Chen, T. H. Lee, and V. Venkataramanan, “Hard Disk Drive Servo Systems,” Springer, 2002.
- [9] A. A. Mamun, G. X. Guo, and B. Bi, “Hard Disk Drive,” Automation and Control Engineering, CRC Press, 2007.
- [10] T. Kamiya, T. Sato, N. Araki, and Y. Konishi, “Ripple rejection for a multirate control system including an integrator,” 5th Int. Symposium on Advanced Control of Industrial Processes (ADCONIP 2014), pp. 170-173, 2D.11, Hiroshima, 2014.
- [11] A. T. Tangirala, D. Li, R. S. Patwardhan, S. L. Shah, and T. Chen, “Ripple-free conditions for lifted multirate control systems,” Automatica, Vol.37, No.10, pp. 1637-1645, 2001.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.