Top > JRM > Linear Quadratic Optimal Regulator for Steady State Drifting o ...

single-rb.php

JRM Vol.27 No.3 pp. 225-234
doi: 10.20965/jrm.2015.p0225
(2015)

Paper:

Views over last 60 days: 1,532

Linear Quadratic Optimal Regulator for Steady State Drifting of Rear Wheel Drive Vehicle

Ronnapee Chaichaowarat and Witaya Wannasuphoprasit†

Department of Mechanical Engineering, Chulalongkorn University
254 Phayathai Road, Wangmai, Pathumwan, Bangkok 10330, Thailand

†Corresponding author

Received:
April 15, 2014
Accepted:
January 28, 2015
Published:
June 20, 2015
Creative Commons License
Keywords:
vehicle dynamics, automotive control, drifting, nonlinear control systems, quadratics optimal regulators
Abstract

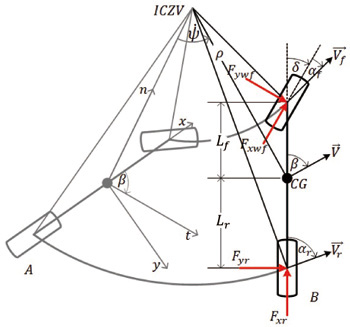
Single-track vehicle drifting
Drifting is a large sideslip cornering technique with counter steering, which is advantageous in some driving conditions where vehicle-handling capability over linear tire slip-friction characteristics is imperative. In this paper, the dynamics of a rear-wheel-drive (RWD) vehicle cornering at steady states was simplified using a single-track vehicle model. In addition, tire frictions in any slip conditions were estimated from the combination of the Pacejka's magic formula and the modified Nicolas-Comstock tire model. A computer program was developed, on the basis of the equations of motion (EOMs) derived via the body-fixed coordinate so that the suitable cornering speed and its corresponding steady-state driving control inputs (the steering angle and rear wheel slip ratio) could be calculated automatically for any given radius of curvature and vehicle sideslip. The other set of EOMs was derived via the normal-tangential coordinate and then linearized so that the state space description could be constructed. Eventually, the linear quadratic optimal regulator was designed and simulated via MATLAB for various regulation problems where the initial condition of each individual state deviated from its desired steady-state value. According to the simulation results, the physical explanation of the control inputs can be used as guidance for adjusting vehicle behavior in manual driving.
Cite this article as:
R. Chaichaowarat and W. Wannasuphoprasit, “Linear Quadratic Optimal Regulator for Steady State Drifting of Rear Wheel Drive Vehicle,” J. Robot. Mechatron., Vol.27 No.3, pp. 225-234, 2015.
Data files:
References
  1. [1] N. Wada, A. Takahashi, M. Saeki, and M. Nishimura, “Vehicle yaw control using an active front steering system with measurements of lateral tire force,” J. of Robotics and Mechatronics, Vol.23, No.1, pp. 83-93, 2011.
  2. [2] T. D. Gillespie, “Fundamentals of Vehicle Dynamics,” SAE Int., PA, USA, 1992.
  3. [3] E. Velenis and P. Tsiotras, “Minimum time vs maximum exit velocity path optimization during cornering,” the IEEE Int. Symposium on Industrial Electronics, 2005.
  4. [4] E. Velenis, P. Tsiotras, and J. Lu, “Modeling aggressive maneuvers on loose surfaces: data analysis and input parameterization,” the Mediterranean Conf. on Control and Automation, 2007.
  5. [5] E. Velenis, P. Tsiotras, and J. Lu, “Modeling aggressive maneuvers on loose surfaces: the cases of trail-braking and pendulum-turn,” the European Control Conf., 2007.
  6. [6] M. Abdulrahim, “On the dynamics of automobile drifting,” SAE Technical Paper, No.2006-01-1019, 2006.
  7. [7] E. Velenis, E. Frazzoli, and P. Tsiotras, “On steady-state cornering equilibria for wheeled vehicles with drift,” the 48th IEEE Conf. on Decision and Control, pp. 3545-3550, 2009.
  8. [8] E. Bakker, L. Nyborg, and H. B. Pacejka, “Tyre modeling for use in vehicle dynamics studies,” SAE Technical Paper, No.870421, 1987.
  9. [9] E. Velenis, D. Katzourakis, E. Frazolli, P. Tsiotras, and R. Happee, “Stabilization of steady-state drifting for a RWD vehicle,” the 10th Int. Symposium on Advanced Vehicle Control, 2010.
  10. [10] E. Velenis, D. Katzourakis, E. Frazolli, P. Tsiotras, and R. Happee, “Steady-state drifting stabilization of RWD vehicles,” Control Engineering Practice, Vol.10, No.11, pp. 1363-1376, 2011.
  11. [11] R. Chaichaowarat and W. Wannasuphoprasit, “Two dimensional dynamic model of drifting vehicle,” the 7th TSAE Int. Conf. on Automotive Engineering, 2011.
  12. [12] R. Chaichaowarat and W. Wannasuphoprasit, “Dynamics and simulation of RWD vehicle drifting at steady state using BNP-MNC tire model,” SAE Technical Paper, No.2013-01-0001, 2013.
  13. [13] R. Chaichaowarat and W. Wannasuphoprasit, “Optimal control for steady state drifting of RWD vehicle,” Proc. of the 7th IFAC Symposium of Advances in Automotive Control, pp. 824-830, 2013.
  14. [14] H. T. Szostak, W. R. Allen, and T. J. Rosenthal, “Analytical modeling of driver response in crash avoidance maneuvering. volume II: an interactive model for driver/vehicle simulation,” U.S. Department of Transportation Report, NHTSA DOT HS-807-271, 1988.
  15. [15] R. Branch and M. Branch, “The tire-force ellipse (friction ellipse) and tire characteristics,” SAE Technical Paper, No.2011-01-0094, 2011.
  16. [16] V. T. Nicolas and T. R. Comstock, “Predicting directional behavior of tractor semitrailers when wheel anti-skid brake systems are used,” ASME Paper, No.72 - WA/AUT-16, 1972.
  17. [17] M. Tanaka, H. Ohtake, and K. Tanaka, “A simple, natural and effective framework of nonlinear systems control and its application to aerial robot,” J. of Robotics and Mechatronics, Vol.26, No.2, pp. 140-147, 2014.

Creative Commons License  This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.

*This site is desgined based on HTML5 and CSS3 for modern browsers, e.g. Chrome, Firefox, Safari, Edge, Opera.

Last updated on Oct. 01, 2024