Paper:
Network-Wide Optimization of Traffic Signals Using Mixed Integer Programming
Md. Abdus Samad Kamal*1, Jun-ichi Imura*2, Tomohisa Hayakawa*2,
Akira Ohata*3, and Kazuyuki Aihara*4
*1Japan Science and Technology Agency and Institute of Industrial Science, The University of Tokyo, 4-6-1 Komaba, Meguro-ku, Tokyo 153-8505, Japan
*2Department of Mechanical and Environmental informatics, Tokyo Institute of Technology, 2-12-1-W8-1 Ookayam, Meguro-ku, Tokyo 152-8552, Japan
*3Toyota Motors Corporation, Sizuoka 410-1107, Japan
*4Institute of Industrial Science, The University of Tokyo, 4-6-1 Komaba, Meguro-ku, Tokyo 153-8505, Japan
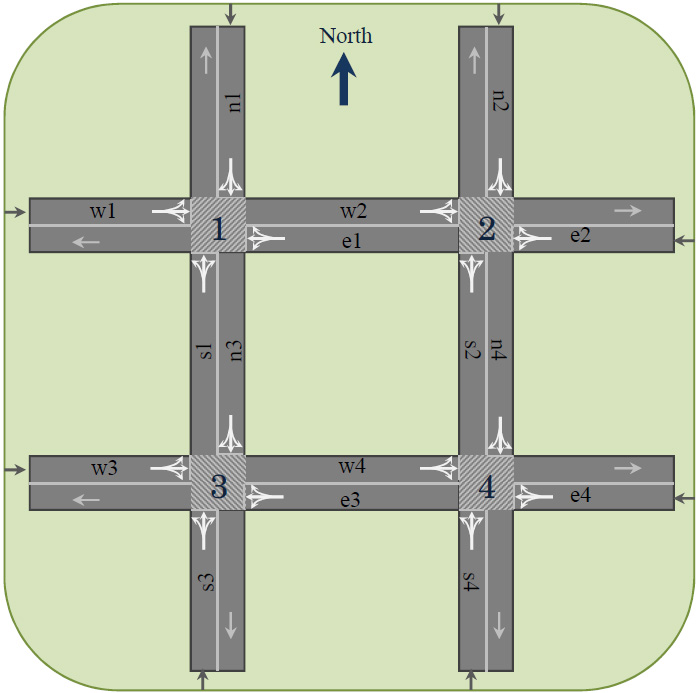 Network with four intersections
Network with four intersections- [1] N. Garber and L. Hoel, “Traffic and highway engineering,” Cengage Learning, Toronto, 4th edition, 2009.
- [2] M. Papageorgiou, C. Diakaki, V. Dinopoulou, A. Kotsialos, and Y. Wang, “Review of road traffic control strategies,” Proc. of the IEEE, Vol.91, No.12, pp. 2043-2067, 2003.
- [3] D. Zhao, Y. Dai, and Z. Zhang, “Computational Intelligence in Urban Traffic Signal Control: A Survey,” IEEE Trans. on Systems, Man, and Cybernetics, Vol.42, No.4, pp. 485-494, 2012.
- [4] P. B. Hunt, D. L. Robertson, and R. D. Bretherton, “The SCOOT on-line traffic signal optimisation technique,” Traffic Engineering and Control, Vol.23, No.4, pp. 190-192, 1982.
- [5] P. Lowrie, “The Sydney coordinated adaptive traffic system: Principles, methodology, algorithms,” Proc. Int. Conf. Road Traffic Signalling, pp. 67-70, 1982.
- [6] D. Robertson and R. Bretherton, “Optimizing networks of traffic signals in real time,” IEEE Trans. on Vehicular Technology, Vol.40, No.1, pp. 11-15, 1991.
- [7] C. Diakaki, M. Papageorgiou, and K. Aboudolas, “A multivariable regulator approach to traffic-responsive network-wide signal control,” Control Engineering Practice, Vol.10, No.2, pp. 183-195, 2002.
- [8] J. Farges, J. Henry, and J. Tufal, “The PRODYN real-time traffic algorithm,” Proc. of the 4th IFAC Symposium on Transportation Systems, pp. 307-312, 1983.
- [9] P. Mirchandani and F. Wang, “RHODES to intelligent transportation systems,” IEEE Intelligent Systems, Vol.20, No.1, pp. 10-15, 2005.
- [10] N. Gartner, “OPAC: a demand-responsive strategy for traffic signal control,” Transportation Research Record, Vol.906, No.75-84, 1983.
- [11] T. Tettamanti, I. Varga, and T. Peni, “MPC in Urban Traffic Management,” In T. Zheng (Ed.), Model Predictive Control, Chapter 8, pp. 251-268, Sciyo InTech, 2010.
- [12] F. Basile, P. Chiacchio, and D. Teta, “A hybrid model for model predictive control of urban traffic,” Proc. of the 9th European Control Conf. (ECC’07), pp. 1823-1830, 2007.
- [13] K. Kim, T. Kato, S. Okuma, and T. Narikiyo, “Traffic network control based on hybrid dynamical system modeling and mixed integer nonlinear programming with convexity analysis,” IEEE Trans. on Systems, Man, and Cybernetics Part A, Vol.38, No.2, pp. 346-357, 2008.
- [14] S. Lin, B. D. Schutter, Y. Xi, and H. Hellendoorn, “Fast model predictive control for urban road networks via MILP,” IEEE Trans. on Intelligent Transportation Systems, Vol.12, No.3, pp. 846-856, 2011.
- [15] M. Berg, A. Hegyi, B. Schutter, and J. Hellendoorn, “A macroscopic traffic flow model for integrated control of freeway and urban traffic networks,” Proc. 42nd IEEE Conf. Decision Control, pp. 2774-2779, 2003.
- [16] H. Khasani and G. Saridis, “Intelligent control for urban traffic systems,” Automatica, Vol.19, No.2, pp. 191-197, 1983.
- [17] M. v. d. Berg, A. Hegyi, B. D. Schutter, and J. Hellendoorn, “Integrated traffic control for mixed urban and freeway networks: A model predictive control approach,” European J. of Transport and Infrastructure Research, Vol.7, No.3, pp. 223-250, 2007.
- [18] M. A. S. Kamal, J. Imura, A. Ohata, T. Hayakawa, and K. Aihara, “Control of Traffic Signals in a Model Predictive Control Framework,” Proc. IFAC Symposium on Control in Transportation Systems, pp. 38-43, 2012.
- [19] M. A. S. Kamal, J. Imura, A. Ohata, T. Hayakawa, and K. Aihara, “Traffic signal control of a road network using MILP in the MPC framework,” In Int. J. of Intelligent Transportation Systems Research, 2014. DOI: 10.1007/s13177-014-0090-3.
- [20] “Aimsun Dynamic Simulator User’s Manual, Version 8,” Transport Simulation Systems, 2012.
- [21] M. A. S. Kamal, J. Imura, A. Ohata, T. Hayakawa, and K. Aihara, “Traffic Signal Control in an MPC Framework Using Mixed Integer Programming,” Proc. IFAC Symposium on Advances in Automotive Control, pp. 641-646, 2013.
- [22] A. Bemporad and M. Morari, “Control of systems integrating logic, dynamics and constraints,” Automatica, Vol.35, No.3, pp. 407-427, 1999.
- [23] A. Atamturk and M. Savelsbergh, “Integer-programming software systems,” Annals of Operations Research, Vol.140, No.1, pp. 67-124, 2005.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.