Research Paper:
Objective-Based Clustering from the Perspective of Transportation Problems: Relevance and Proposal of a New Clustering Method
Yasunori Endo†
 and Kana Kayama
and Kana Kayama
University of Tsukuba
1-1-1 Tennodai, Tsukuba, Ibaraki 305-8573, Japan
†Corresponding author
This paper discusses objective-based clustering, represented by hard -means and fuzzy c-means (FCM) methods, from two perspectives. The first is the relationship between transportation problems and objective-based clustering. The transportation problem involves determining the amount of transportation from a supply location to a demand location to minimize the total transportation cost, given the respective supply and demand quantities and the respective transportation costs from the supply location to the demand location for given multiple supply and demand locations. In this study, we demonstrate a theoretical connection between transportation problems and objective-based clustering. The second is the proposal of a new clustering method that focuses on the first argument. First, by focusing on the transportation problem, we discuss the problem of defuzzification in methods that introduce fuzzy concepts, including FCM, that is mainstream in objective-based clustering, and propose an index to evaluate the clustering results from the perspective of defuzzification. Subsequently, we propose a new clustering algorithm based on this index. Moreover, we evaluate the performance of the proposed method using numerical examples.
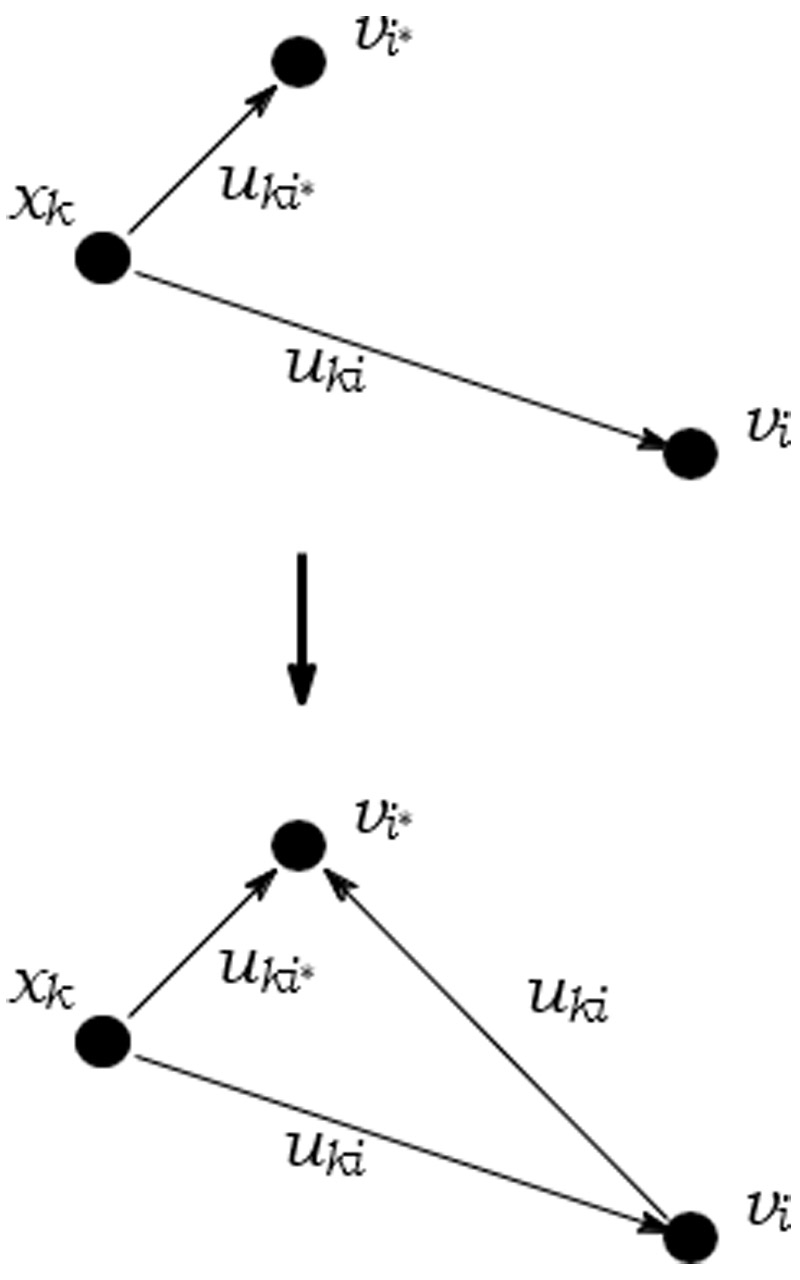
Membership degree from the perspective of the transportation problem
- [1] F. Cavalletti, “An Overview of L1 Optimal Transportation on Metric Measure Spaces,” Nicola Gigli (Ed.), “Measure Theory in Non-Smooth Spaces,” pp. 98-144, De Gruyter, 2017. https://doi.org/10.1515/9783110550832-003
- [2] G. Monge, “Mémoire sur la théorie des déblais et des remblais,” Imprimerie Royale, 1781.
- [3] F. L. Hitchcock, “The Distribution of a Product from Several Sources to Numerous Localities,” J. of Mathematics and Physics, Vol.20, pp. 224-230, 1941. https://doi.org/10.1002/sapm1941201224
- [4] J. B. MacQueen, “Some Methods for classification and Analysis of Multivariate Observations,” Proc. of 5th Berkeley Symp. on Mathematical Statistics and Probability, pp. 281-297, 1967.
- [5] J. C. Dunn, “A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters,” J. of Cybernetics, Vol.3, No.3, pp. 32-57, 1973. https://doi.org/10.1080/01969727308546046
- [6] J. C. Dunn, “Well-Separated Clusters and Optimal Fuzzy Partitions,” J. of Cybernetics. Vol.4, No.1, pp. 95-104, 1973. https://doi.org/10.1080/01969727408546059
- [7] J. C. Bezdek, “Fuzzy Mathematics in Pattern Classification,” Ph.D. thesis, Cornell University, 1973.
- [8] J. C. Bezdek, “Pattern Recognition with Fuzzy Objective Function Algorithms,” Springer, 1981. https://doi.org/10.1007/978-1-4757-0450-1
- [9] Y. Endo, T. Hirano, N. Kinoshita, and Y. Hamasuna, “On Various Types of Even-sized Clustering Based on Optimization,” The 13th Int. Conf. on Modeling Decisions for Artificial Intelligence (MDAI 2016), pp. 165-177, 2016. https://doi.org/10.1007/978-3-319-45656-0_14
- [10] Y. Endo, S. Ishida, and N. Kinoshita, “Controlled-sized Clustering Based on Optimization,” Joint 17th World Congress of Int. Fuzzy Systems Association and 9th Int. Conf. on Soft Computing and Intelligent Systems (IFSA-SCIS 2017), 2017. https://doi.org/10.1109/IFSA-SCIS.2017.8023341
- [11] K. Kitajima and Y. Endo, “A Note on Fuzzified Even-Sized Clustering Based on Optimization,” Proc. of 2017 Conf. of the Int. Federation of Classification Societies (IFCS 2017), 2017.
- [12] S. Miyamoto, K. Umayahara, and M. Mukaidono, “Fuzzy Classification Functions in the Methods of Fuzzy c-Means and Regularization by Entropy,” J. of Japan Society for Fuzzy Theory and Systems, Vol.10, No.3, pp. 548-557, 1998 (in Japanese). https://doi.org/10.3156/jfuzzy.10.3_548
- [13] R. Krishnapuram and J. M. Keller, “A possibilistic Approach to Clustering,” IEEE Trans. on Fuzzy Systems, Vol.1, No.2, pp. 98-110, 1993. https://doi.org/10.1109/91.227387
- [14] UC Irvine Machine Learning Repository. https://archive.ics.uci.edu/dataset/53/iris [Accessed April 17, 2025]
- [15] L. N. Vaserstein, “Markov Processes over Denumerable Products of Spaces, Describing Large Systems of Automata,” Problemy Peredači Informacii, Vol.5, No.3, pp. 64-72, 1969 (in Russian).
- [16] L. Kantorovich, “On the Translocation of Masses,” Proc. of the Academy of Sciences of the USSR (Doklady Akademii Nauk SSSR), Vol.37, Nos.7-8, pp. 199-201, 1942 (in Russian).
- [17] T. Fukunaga and H. Kasai, “Wasserstein k-Means with Sparse Simplex Projection,” 25th Int. Conf. on Pattern Recognition (ICPR), pp. 1627-1634, 2020. https://doi.org/10.1109/ICPR48806.2021.9412131
- [18] R. Rao, A. Moscovich, and A. Singer, “Wasserstein k-Means for Clustering Tomographic Projections,” Machine Learning for Structural Biology Workshop, 2020.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.