Research Paper:
Efficient Tournament Selection Using Data Envelopment Analysis in Multiobjective Genetic Algorithms with Pareto Front Modeling and Reference Pairing
Mamoru Doi*
 , Kenya Sugihara*, and Masao Arakawa**
, Kenya Sugihara*, and Masao Arakawa**

*Mitsubishi Electric Corporation
5-1-1 Ofuna, Kamakura, Kanagawa 247-8501, Japan
**Waseda University
2-7 Hibikino, Wakamatsu-ku, Kitakyushu, Fukuoka 808-0135, Japan
In the real world, multiobjective optimization problems require the efficient acquisition of diverse solutions. Various multiobjective evolutionary algorithms (MOEAs) have been developed to address these problems. Typically, MOEAs use the same scoring criteria for both survival and mating selection, despite their different roles. Survival selection should ensure convergence and diversity, whereas mating selection should focus on selecting individuals with higher convergence for crossover. In this article, an efficient selection algorithm is proposed that integrates data envelopment analysis (DEA), Pareto front modeling, and a reference crossover mechanism. In survival selection, algorithms are used to ensure high convergence and diversity. In a previous study, DEA was employed to select individuals with higher convergence in mating selection. This approach balances convergence and diversity. In addition, Pareto front modeling addresses the convexity assumption issue in DEA. In this study, by selecting constraint solutions obtained through DEA as crossover targets, the algorithm makes crossover with superior solutions possible, enhancing optimization speed and diversity. The algorithm is particularly effective for benchmark functions that benefit from neighborhood crossover. In comparisons using the hypervolume metric on the WFG and DTLZ benchmark functions, the proposed algorithm outperformed NSGA-II, NSGA-III, AGE-MOEA-II, DEA-GA, MOEA/D, and other previous algorithms. The results of a Wilcoxon rank-sum test also showed that the proposed algorithm is statistically superior.
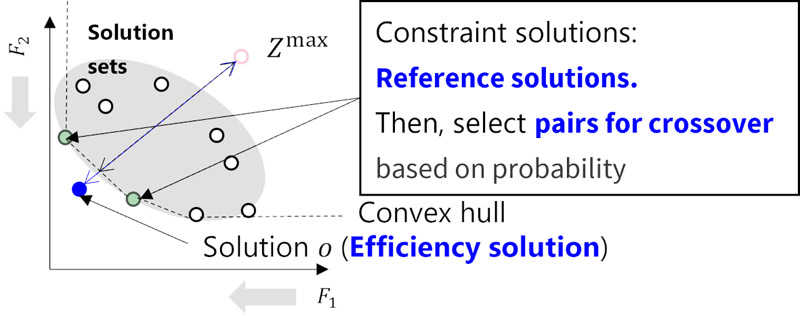
Concept of PF modeling DEA selection GA with reference pairing
- [1] J. D. Schaffer, “Multiple objective optimization with vector evaluated genetic algorithms,” Proc. of the 1st Int. Conf. on Genetic Algorithms, pp. 93-100, 1985.
- [2] C. M. Fonseca and P. J. Fleming, “Multiobjective genetic algorithms,” IEE Colloquium on Genetic Algorithms for Control Systems Engineering, 1993.
- [3] J. Horn, N. Nafpliotis, and D. E. Goldberg, “A niched Pareto genetic algorithm for multiobjective optimization,” Proc. of the 1st IEEE Conf. on Evolutionary Computation, Vol.1, pp. 82-87, 1994. https://doi.org/10.1109/ICEC.1994.350037
- [4] N. Srinivas and K. Deb, “Muiltiobjective optimization using nondominated sorting in genetic algorithms,” Evolutionary Computation, Vol.2, No.3, pp. 221-248, 1994. https://doi.org/10.1162/evco.1994.2.3.221
- [5] K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Trans. on Evolutionary Computation, Vol.6, No.2, pp. 182-197, 2002. https://doi.org/10.1109/4235.996017
- [6] Q. Zhang and H. Li, “MOEA/D: A multiobjective evolutionary algorithm based on decomposition,” IEEE Trans. on Evolutionary Computation, Vol.11, No.6, pp. 712-731, 2007. https://doi.org/10.1109/TEVC.2007.892759
- [7] H. Li and Q. Zhang, “Multiobjective optimization problems with complicated Pareto sets, MOEA/D and NSGA-II,” IEEE Trans. on Evolutionary Computation, Vol.13, No.2, pp. 284-302, 2008. https://doi.org/10.1109/TEVC.2008.925798
- [8] K. Deb and J. Sundar, “Reference point based multi-objective optimization using evolutionary algorithms,” Proc. of the 8th Annual Conf. on Genetic and Evolutionary Computation, pp. 635-642, 2006. https://doi.org/10.1145/1143997.1144112
- [9] K. Deb and H. Jain, “An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part i: Solving problems with box constraints,” IEEE Trans. on Evolutionary Computation, Vol.18, No.4, pp. 577-601, 2014. https://doi.org/10.1109/TEVC.2013.2281535
- [10] H. Jain and K. Deb, “An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part ii: Handling constraints and extending to an adaptive approach,” IEEE Trans. on Evolutionary Computation, Vol.18, No.4, pp. 602-622, 2014. https://doi.org/10.1109/TEVC.2013.2281534
- [11] Y. Vesikar, K. Deb, and J. Blank, “Reference point based NSGA-III for preferred solutions,” 2018 IEEE Symp. Series on Computational Intelligence, pp. 1587-1594, 2018. https://doi.org/10.1109/SSCI.2018.8628819
- [12] A. Panichella, “An adaptive evolutionary algorithm based on non-Euclidean geometry for many-objective optimization,” Proc. of the Genetic and Evolutionary Computation Conf., pp. 595-603, 2019. https://doi.org/10.1145/3321707.3321839
- [13] A. Panichella, “An improved Pareto front modeling algorithm for large-scale many-objective optimization,” Proc. of the Genetic and Evolutionary Computation Conf., pp. 565-573, 2022. https://doi.org/10.1145/3512290.3528732
- [14] A. Konak, D. W. Coit, and A. E. Smith, “Multi-objective optimization using genetic algorithms: A tutorial,” Reliability Engineering & System Safety, Vol.91, No.9, pp. 992-1007, 2006. https://doi.org/10.1016/j.ress.2005.11.018
- [15] K. Deb, “Multi-objective optimisation using evolutionary algorithms: An introduction,” L. Wang, A. H. C. Ng, and K. Deb (Eds.), “Multi-Objective Evolutionary Optimisation for Product Design and Manufacturing,” pp. 3-34, Springer, 2011. https://doi.org/10.1007/978-0-85729-652-8_1
- [16] K. Deb, “Multi-objective evolutionary algorithms,” J. Kacprzyk and W. Pedrycz (Eds.), “Springer Handbook of Computational Intelligence,” pp. 995-1015, Springer, 2015. https://doi.org/10.1007/978-3-662-43505-2_49
- [17] Z. Liu, F. Han, Q. Ling, H. Han, and J. Jiang, “A many-objective optimization evolutionary algorithm based on hyper-dominance degree,” Swarm and Evolutionary Computation, Vol.83, Article No.101411, 2023. https://doi.org/10.1016/j.swevo.2023.101411
- [18] Y. Yun, H. Nakayama, T. Tanino, and M. Arakawa, “A multi-objective optimization method combining generalized data envelopment analysis and genetic algorithms,” Trans. of the Institute of Systems, Control and Information Engineers, Vol.13, No.4, pp. 179-185, 2000 (in Japanese). https://doi.org/10.5687/iscie.13.4_179
- [19] E. Takeda, “An extended DEA model: Appending an additional input to make all DMUs at least weakly efficient,” European J. of Operational Research, Vol.125, No.1, pp. 25-33, 2000. https://doi.org/10.1016/S0377-2217(99)00195-2
- [20] A. Charnes, W. W. Cooper, and E. Rhodes, “Measuring the efficiency of decision making units,” European J. of Operational Research, Vol.2, No.6, pp. 429-444, 1978. https://doi.org/10.1016/0377-2217(78)90138-8
- [21] M. Doi, T. Onishi, and M. Arakawa, “Genetic algorithm with efficient selection using data envelopment analysis,” Proc. of the Japanese Society for Evolutionary Computation, pp. 116-135, 2023.
- [22] M. Doi, K. Sugihara, and M. Arakawa, “Genetic algorithm with efficient selection using Pareto front modeling and data envelopment analysis,” 2024 Joint 13th Int. Conf. on Soft Computing and Intelligent Systems and 25th Int. Symp. on Advanced Intelligent Systems, 2024. https://doi.org/10.1109/SCISISIS61014.2024.10760104
- [23] S. Watanabe, T. Hiroyasu, and M. Miki, “NCGA: Neighborhood cultivation genetic algorithm for multi-objective optimization problems,” GECCO Late Breaking Papers, pp. 458-465, 2002.
- [24] H. Ishibuchi, N. Akedo, and Y. Nojima, “Relation between neighborhood size and MOEA/D performance on many-objective problems,” Proc. of the 7th Int. Conf. on Evolutionary Multi-Criterion Optimization, pp. 459-474, 2013. https://doi.org/10.1007/978-3-642-37140-0_35
- [25] J. Blank and K. Deb, “Pymoo: Multi-objective optimization in Python,” IEEE Access, Vol.8, pp. 89497-89509, 2020. https://doi.org/10.1109/ACCESS.2020.2990567
- [26] C. M. Fonseca, L. Paquete, and M. Lopez-Ibanez, “An improved dimension-sweep algorithm for the hypervolume indicator,” 2006 IEEE Int. Conf. on Evolutionary Computation, pp. 1157-1163, 2006. https://doi.org/10.1109/CEC.2006.1688440
- [27] H. Ishibuchi, H. Masuda, Y. Tanigaki, and Y. Nojima, “Modified distance calculation in generational distance and inverted generational distance,” Proc. of the 8th Int. Conf. on Evolutionary Multi-Criterion Optimization, pp. 110-125, 2015. https://doi.org/10.1007/978-3-319-15892-1_8
- [28] K. Deb and R. B. Agrawal, “Simulated binary crossover for continuous search space,” Complex Systems, Vol.9, No.2, pp. 115-148, 1995.
- [29] K. Deb, K. Sindhya, and T. Okabe, “Self-adaptive simulated binary crossover for real-parameter optimization,” Proc. of the 9th Annual Conf. on Genetic and Evolutionary Computation, pp. 1187-1194, 2007. https://doi.org/10.1145/1276958.1277190
- [30] H. Ishibuchi, Y. Setoguchi, H. Masuda, and Y. Nojima, “Performance of decomposition-based many-objective algorithms strongly depends on Pareto front shapes,” IEEE Trans. on Evolutionary Computation, Vol.21, No.2, pp. 169-190, 2017. https://doi.org/10.1109/TEVC.2016.2587749
- [31] H. Ishibuchi, Y. Nan, and L. M. Pang, “Performance evaluation of multi-objective evolutionary algorithms using artificial and real-world problems,” Proc. of the 12th Int. Conf. on Evolutionary Multi-Criterion Optimization, pp. 333-347, 2023. https://doi.org/10.1007/978-3-031-27250-9_24
- [32] L. M. Pang, H. Ishibuchi, and K. Shang, “Analysis of algorithm comparison results on real-world multi-objective problems,” 2024 IEEE Congress on Evolutionary Computation, 2024. https://doi.org/10.1109/CEC60901.2024.10612187
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.