Research Paper:
Revised Margin-Maximization Method for Nearest Prototype Classifier Learning
Yoshifumi Kusunoki
 and Tomoharu Nakashima
and Tomoharu Nakashima

Graduate School of Informatics, Osaka Metropolitan University
1-1 Gakuen-cho, Naka-ku, Sakai, Osaka 599-8531, Japan
This paper proposes a revised margin-maximization method for training nearest prototype classifiers (NPCs), which are known as an explainable supervised learning model. The margin-maximization method of our previous study formulates NPC training as a difference-of-convex (DC) programming problem solved via the convex-concave procedure. However, it suffers from issues related to hyperparameter sensitivity and its inability to simultaneously optimize both classification and clustering performances. To overcome these drawbacks, the revised method directly solves the margin-maximization problem using a method of sequential second-order cone programming, without DC programming reduction. Furthermore, it integrates clustering loss from the k-means method into the objective function to enhance prototype placement in dense data regions. We prove that the revised method is a descent algorithm, that is, the objective function decreases in each update of the solution. A numerical study confirms that the revised method addresses the drawbacks of the previous method.
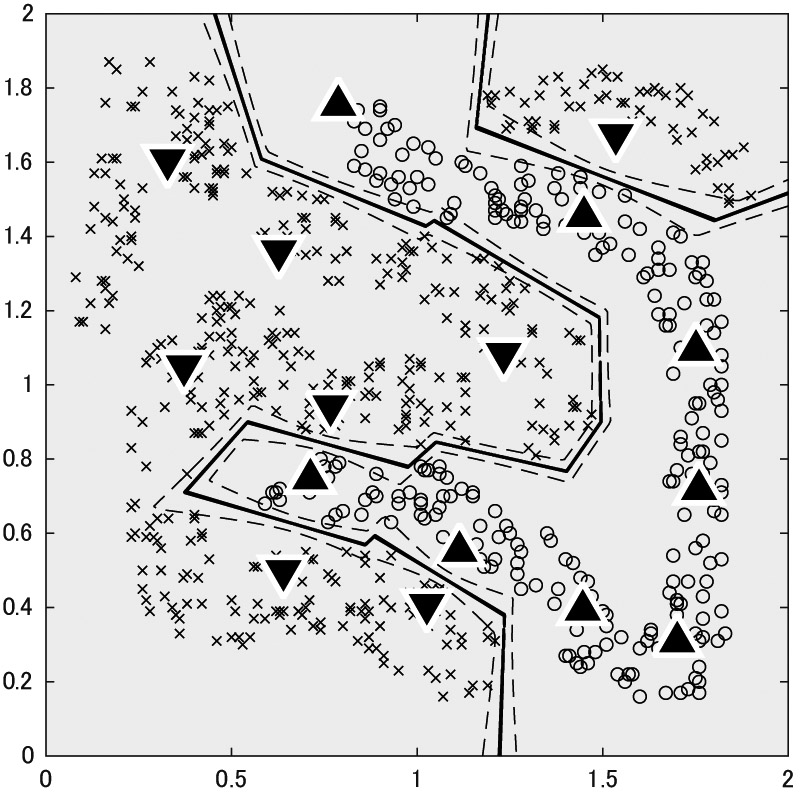
Maximum-margin nearest prototype classifier
- [1] I. Triguero, J. Derrac, S. Garcia, and F. Herrera, “A Taxonomy and Experimental Study on Prototype Generation for Nearest Neighbor Classification,” IEEE Trans. on Systems, Man, and Cybernetics, Part C (Applications and Reviews), Vol.42, Issue 1, pp. 86-100, 2012. https://doi.org/10.1109/TSMCC.2010.2103939
- [2] T. Kohonen, “The self-organizing map,” Proc. of the IEEE, Vol.78, Issue 9, pp. 1464-1480, 1990. https://doi.org/10.1109/5.58325
- [3] A. Sato and K. Yamada, “Generalized learning vector quantization,” Proc. of the 9th Int. Conf. on Neural Information Processing Systems (NIPS’95), pp. 423-429, 1995.
- [4] X.-B. Jin, C.-L. Liu, and X. Hou, “Regularized margin-based conditional log-likelihood loss for prototype learning,” Pattern Recognition, Vol.43, Issue 7, pp. 2428-2438, 2010. https://doi.org/10.1016/j.patcog.2010.01.013
- [5] Y. Kusunoki, C. Wakou, and K. Tatsumi, “Maximum-Margin Model for Nearest Prototype Classifiers,” J. Adv. Comput. Intell. Intell. Inform., Vol.22, No.4, pp. 565-577, 2018. https://doi.org/10.20965/jaciii.2018.p0565
- [6] T. Lipp and S. Boyd, “Variations and extension of the convex–concave procedure,” Optimization and Engineering, Vol.17, No.2, pp. 263-287, 2016. https://doi.org/10.1007/s11081-015-9294-x
- [7] Y. Kusunoki and T. Nakashima, “Revised Optimization Algorithm for Maximum-Margin Nearest Prototype Classifier,” The 20th World Congress of the Int. Fuzzy Systems Association (IFSA 2023), pp. 276-280, 2023.
- [8] Y. Kusunoki, “Maximum-Margin Nearest Prototype Classifiers with the Sum-over-Others Loss Function and a Performance Evaluation,” K. Honda, B. Le, V.-N. Huynh, M. Inuiguchi, and Y. Kohda (Eds.), “Integrated Uncertainty in Knowledge Modelling and Decision Making,” pp. 37-46, Springer, 2023. https://doi.org/10.1007/978-3-031-46781-3_4
- [9] H. Kato and M. Fukushima, “An SQP-type algorithm for nonlinear second-order cone programs,” Optimization Letters, Vol.1, No.2, pp. 129-144, 2007. https://doi.org/10.1007/s11590-006-0009-2
- [10] D. Arthur and S. Vassilvitskii, “k-means++: The advantages of careful seeding,” Proc. of the 18th Annual ACM-SIAM Symp. on Discrete Algorithms (SODA’07), pp. 1027-1035, 2007.
- [11] J. Borwein and A. Lewis, “Convex Analysis and Nonlinear Optimization: Theory and Examples,” CMS Books in Mathematics, Springer, 2005. https://doi.org/10.1007/978-0-387-31256-9
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.