Development Report:
Inclusion–Exclusion Integral Neural Networks: A Framework for Explainable AI with Non-Additive Measures
Yoshihiro Fukushima*1, Katsushige Fujimoto*2
 , Simon James*3
, Simon James*3
 , and Aoi Honda*4
, and Aoi Honda*4

*1NEC Solution Innovators, Ltd.
1-18-7 Shin-Kiba, Koto-ku, Tokyo 136-8627, Japan
*2Fukushima University
1 Kanayagawa, Fukushima, Fukushima 960-1296, Japan
*3Deakin University
221 Burwood Highway, Burwood, Victoria 3125, Australia
*4Kyushu Institute of Technology
680-4 Kawazu, Iizuka, Fukuoka 820-8502, Japan
This study introduces the inclusion–exclusion integral neural network (IEINN) and its accompanying open-source Python library, a novel framework designed to enhance the interpretability of neural networks by leveraging non-additive monotone measures and polynomial operations. The proposed architecture integrates the inclusion–exclusion integral into the network structure, enabling direct extraction of structured information from the learned parameters. We develop a Python-based IEINN library, implemented using PyTorch, to facilitate efficient model training and integration. The library includes several preprocessing methods for parameter initialization, such as normalization based on minimum and maximum values, percentiles, and standard deviations, which enhance training stability and convergence. Additionally, the framework supports various computational operations, including t-norms and t-conorms, allowing flexible modeling of interactions among input variables. The proposed framework is publicly available as an open-source library on GitHub (AoiHonda-lab/IEI-NeuralNetwork), facilitating further research and practical applications in explainable AI.
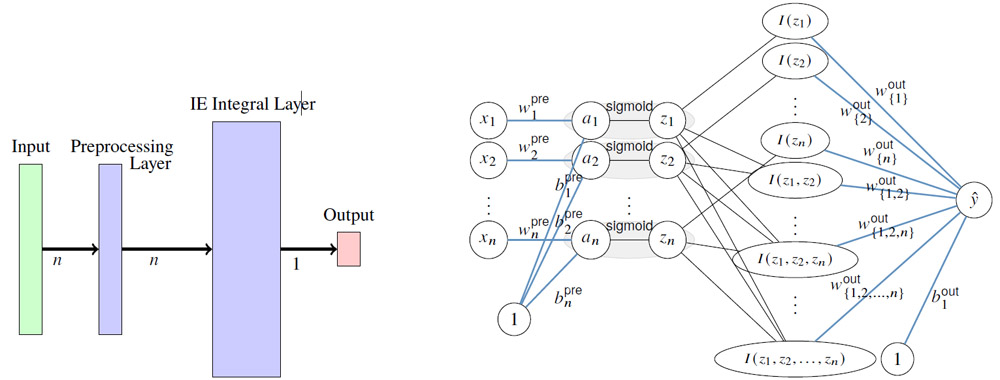
Architecture of the IE-Iintegral NN
- [1] Y. LeCun, Y. Bengio, and G. Hinton, “Deep learning,” Nature, Vol.521, No.7553, pp. 436-444, 2015. https://doi.org/10.1038/nature14539
- [2] A. Krizhevsky, I. Sutskever, and G. E. Hinton, “Imagenet classification with deep convolutional neural networks,” Advances in Neural Information Processing Systems (NIPS), Vol.25, pp. 1097-1105, 2012.
- [3] Z. C. Lipton, “The mythos of model interpretability,” arXiv preprint, arXiv:1606.03490, 2016. https://doi.org/10.48550/arXiv.1606.03490
- [4] M. T. Ribeiro, S. Singh, and C. Guestrin, “Why should I trust you? Explaining the predictions of any classifier,” Proc. of the 22nd ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, pp. 1135-1144, 2016. https://doi.org/10.1145/2939672.2939778
- [5] R. Caruana et al., “Intelligible models for healthcare: Predicting pneumonia risk and hospital 30-day readmission,” Proc. of the 21st ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, pp. 1721-1730, 2015. https://doi.org/10.1145/2939672.2939778
- [6] K. R. Varshney, “Trustworthy machine learning and artificial intelligence,” XRDS: Crossroads, The ACM Magazine for Students, Vol.25, No.3, pp. 26-29, 2019. https://doi.org/10.1145/3313109
- [7] F. Doshi-Velez and B. Kim, “Towards a rigorous science of interpretable machine learning,” arXiv preprint, arXiv:1702.08608, 2017. https://doi.org/10.48550/arXiv.1702.08608
- [8] S. M. Lundberg and S.-I. Lee, “A unified approach to interpreting model predictions,” Advances in Neural Information Processing Systems (NIPS), Vol.30, pp. 4768-4777, 2017.
- [9] M. T. Ribeiro, S. Singh, and C. Guestrin, “Model-Agnostic Interpretability of Machine Learning,” arXiv preprint, arXiv:1606.05386, 2016. https://doi.org/10.48550/arXiv.1606.05386
- [10] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser, and I. Polosukhin, “Attention is all you need,” Advances in Neural Information Processing Systems (NIPS), Vol.30, pp. 6000-6010, 2017.
- [11] C. Rudin, “Stop explaining black-box machine learning models for high stakes decisions and use interpretable models instead,” Nature Machine Intelligence, Vol.1, No.5, pp. 206-215, 2019. https://doi.org/10.1038/s42256-019-0048-x
- [12] A. Honda and Y. Okazaki, “Theory of inclusion-exclusion integral,” Information Sciences, Vol.376, pp. 136-147, 2017. https://doi.org/10.1016/j.ins.2016.09.063
- [13] A. Honda, M. Itabashi, and S. James, “A neural network based on the inclusion-exclusion integral and its application to data analysis,” Information Sciences, Vol.648, Article No.119549, 2023. https://doi.org/10.1016/j.ins.2023.119549
- [14] https://github.com/AoiHonda-lab/IEI-NeuralNetwork [Accessed November 2, 2025]
- [15] M. Bohanec and V. Rajkovič, “Car Evaluation Data Set,” UCI Machine Learning Repository, 1997. https://archive.ics.uci.edu/ml/datasets/Car+Evaluation [Accessed November 2, 2025]
- [16] B. Schweizer and A. Sklar, “Associative functions and statistical triangle inequalities,” Publ. Math. Debrecen, Vol.8, pp. 169-186, 1961. https://doi.org/10.5486/pmd.1961.8.1-2.16
- [17] E. P. Klement, R. Mesiar, and E. Pap, “Triangular Norms,” Kluwer Academic Publishers, 2000. https://doi.org/10.1007/978-94-015-9540-7
- [18] G. Mayor and J. Torrens, “Duality for a class of binary operators on [0,1],” Fuzzy Sets and Systems, Vol.47, No.1, pp. 77-80, 1992. https://doi.org/10.1016/0165-0114(92)90061-8
- [19] L. S. Shapley, “A value for n-person games,” H. W. Kuhn and A. W. Tucker (Eds.), Contributions to the Theory of Games, Vol.II, pp. 307-317, Princeton University Press, 1953. https://doi.org/10.1515/9781400881970-018
- [20] A. Honda and M. Grabisch, “Entropy of capacities on lattices and set systems,” Information Sciences Vol.176, No.23, pp. 3472-3489, 2006. https://doi.org/10.1016/j.ins.2006.02.011
- [21] M. Grabisch, “k-order additive discrete fuzzy measures and their representation,” Fuzzy Sets and Systems, Vol.92, No.2, pp. 167-189, 1997. https://doi.org/10.1016/S0165-0114(97)00168-1
- [22] A. E. Hoerl and R. W. Kennard, “Ridge regression: Biased estimation for nonorthogonal problems,” Technometrics, Vol.12, No.1, pp. 55-67, 1970. https://doi.org/10.2307/1267351
- [23] R. Tibshirani, “Regression shrinkage and selection via the Lasso,” J. of the Royal Statistical Society: Series B (Methodological), Vol.58, No.1, pp. 267-288, 1996. https://doi.org/10.1111/j.2517-6161.1996.tb02080.x
- [24] H. Anai, S. James, and A. Honda, “Inclusion–Exclusion integral neural network using monotone regularization terms,” Proc. of the 21st Int. Conf. on Modeling Decisions for Artificial Intelligence, pp. 42-53, 2024.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.