Research Paper:
Optimal Consensus Control for Switching Uncertain Multiagent Systems Using Model Reference Control and Reinforcement Learning
Wenpeng He*,**,***
 , Xin Chen*,**,***,†
, Xin Chen*,**,***,†
 , and Yipu Sun*,**,***
, and Yipu Sun*,**,***

*School of Automation, China University of Geosciences
No.388 Lumo Road, Hongshan District, Wuhan 430074, China
**Hubei Key Laboratory of Advanced Control and Intelligent Automation for Complex Systems
No.388 Lumo Road, Hongshan District, Wuhan 430074, China
***Engineering Research Center of Intelligent Technology for Geo-Exploration, Ministry of Education
No.388 Lumo Road, Hongshan District, Wuhan 430074, China
†Corresponding author
This paper addresses the optimal consensus problem in uncertain switching multiagent systems. The inherent uncertainty and time-varying structure of local tracking error system render conventional methods ineffective for deriving optimal control protocols. To overcome these challenges, we introduce a reference model for each agent and construct a modified augmented local tracking error (ALTE) system. This approach transforms the optimal consensus problem into two sub-problems: 1) model reference control (MRC) between agents and their reference models; 2) distributed optimal stabilization of the modified ALTE system. We propose a new control scheme that combines filtered tracking error with equivalent input disturbance method to achieve MRC. To realize distributed optimal stabilization of the modified ALTE, we introduce a deep deterministic policy gradient method based on value iteration. Through theoretical analysis, we demonstrate that the multiagent system achieves a near Nash equilibrium, which is further validated by numerical simulation.
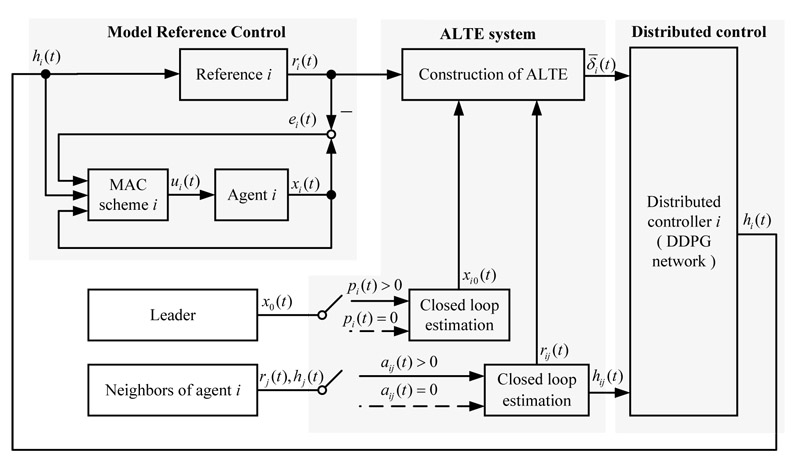
A novel hierarchical control structure for uncertain multi-agent systems
- [1] P. Lu, W. Yu, G. Chen, and X. Yu, “Leaderless Consensus of Ring-Networked Mobile Robots via Distributed Saturated Control,” IEEE Trans. on Industrial Electronics, Vol.67, No.12, pp. 10723-10731, 2020. https://doi.org/10.1109/TIE.2019.2960729
- [2] F. L. D. Silva, C. E. H. Nishida, D. M. Roijers, and A. H. R. Costa, “Coordination of Electric Vehicle Charging Through Multiagent Reinforcement Learning,” IEEE Trans. on Smart Grid, Vol.11, No.3, pp. 2347-2356, 2020. https://doi.org/10.1109/TSG.2019.2952331
- [3] H. Hattori, Y. Nakajima, and S. Yamane, “Massive Multiagent-Based Urban Traffic Simulation with Fine-Grained Behavior Models,” J. Adv. Comput. Intell. Intell. Inform., Vol.15, No.2, pp. 233-239, 2011. https://doi.org/10.20965/jaciii.2011.p0233
- [4] R. Qian, Z. Duan, Y. Qi, T. Peng, and W. Wang, “Formation-Control Stability and Communication Capacity of Multiagent Systems: A Joint Analysis,” IEEE Trans. on Control of Network Systems, Vol.8, No.2, pp. 917-927, 2021. https://doi.org/10.1109/TCNS.2020.3015028
- [5] S. He, X. Liu, P. Lu, C. Du, and H. Liu, “Distributed Finite-Time Consensus Algorithm for Multiagent Systems via Aperiodically Intermittent Protocol,” IEEE Trans. on Circuits and Systems II: Express Briefs, Vol.69, No.7, pp. 3229-3233, 2022. https://doi.org/10.1109/TCSII.2021.3135866
- [6] W. Ren and R. W. Beard, “Consensus seeking in multiagent systems under dynamically changing interaction topologies,” IEEE Trans. on Automatic Control, Vol.50, No.5, pp. 655-661, 2005. https://doi.org/10.1109/TAC.2005.846556
- [7] Y. Su and J. Huang, “Two consensus problems for discrete-time multiagent systems with switching network topology,” Automatica, Vol.48, No.9, pp. 1988-1997, 2012. https://doi.org/10.1016/j.automatica.2012.03.029
- [8] Y. Su and J. Huang, “Stability of a class of linear switching systems with applications to two consensus problems,” IEEE Trans. on Automatic Control, Vol.57, No.6, pp. 1420-1430, 2011. https://doi.org/10.1109/TAC.2011.2176391
- [9] X. Mu, X. Xiao, K. Liu, and J. Zhang, “Leader-following consensus of multiagent systems with jointly connected topology using distributed adaptive protocols,” J. of the Franklin Institute, Vol.351, No.12, pp. 5399-5410, 2014. https://doi.org/10.1016/j.jfranklin.2014.09.018
- [10] C. He and J. Huang, “Adaptive distributed observer for general linear leader systems over periodic switching digraphs,” Automatica, Vol.137, Article No.110021, 2022. https://doi.org/10.1016/j.automatica.2021.110021
- [11] J. Zhang, H. Zhang, Y. Liang, and W. Song, “Adaptive bipartite output tracking consensus in switching networks of heterogeneous linear multiagent systems based on edge events,” IEEE Trans. on Neural Networks and Learning Systems, Vol.34, No.1, pp. 79-89, 2021. https://doi.org/10.1109/TNNLS.2021.3089596
- [12] M. I. Abouheaf, F. L. Lewis, K. G. Vamvoudakis et al., “Multi-agent discrete-time graphical games and reinforcement learning solutions,” Automatica, Vol.50, No.12, pp. 3038-3053, 2014. https://doi.org/10.1016/j.automatica.2014.10.047
- [13] K. G. Vamvoudakis, F. L. Lewis, and G. R. Hudas, “Multi-agent differential graphical games: Online adaptive learning solution for synchronization with optimality,” Automatica, Vol.48, No.8, pp. 1598-1611, 2012. https://doi.org/10.1016/j.automatica.2012.05.074
- [14] J. Zhang, Z. Wang, and H. Zhang, “Data-based optimal control of multiagent systems: A reinforcement learning design approach,” IEEE Trans. on Cybernetics, Vol.49, No.12, pp. 4441-4449, 2018. https://doi.org/10.1109/TCYB.2018.2868715
- [15] Z. Peng, Y. Zhao, J. Hu et al., “Input–output data-based output antisynchronization control of multiagent systems using reinforcement learning approach,” IEEE Trans. on Industrial Informatics, Vol.17, No.11, pp. 7359-7367, 2021. https://doi.org/10.1109/TII.2021.3050768
- [16] H. Fu, X. Chen, W. Wang et al., “Data-based optimal synchronization control for discrete-time nonlinear heterogeneous multiagent systems,” IEEE Trans. on Cybernetics, Vol.52, No.4, pp. 2477-2490, 2020. https://doi.org/10.1109/TCYB.2020.3004494
- [17] W. He, X. Chen, and H. Fu, “Dual ML-ADHDP method for heterogeneous discrete-time nonlinear multiagent systems with unknown dynamics and time delay,” J. of the Franklin Institute, Vol.359, No.11, pp. 5634-5657, 2022. https://doi.org/10.1016/j.jfranklin.2022.04.040
- [18] Z. Ni, H. He, and J. Wen, “Adaptive Learning in Tracking Control Based on the Dual Critic Network Design,” IEEE Trans. on Neural Networks and Learning Systems, Vol.24, No.6, pp. 913-928, 2013. https://doi.org/10.1109/TNNLS.2013.2247627
- [19] H. Fu, X. Chen, W. Wang et al., “MRAC for unknown discrete-time nonlinear systems based on supervised neural dynamic programming,” Neurocomputing, Vol.384, pp. 130-141, 2020. https://doi.org/10.1016/j.neucom.2019.12.023
- [20] M. S. Ahmed, “Neural net based MRAC for a class of nonlinear plants,” Neural networks, Vol.13, No.1, pp. 111-124, 2000. https://doi.org/10.1016/s0893-6080(99)00082-9
- [21] X. Chen and H. Fu, “Distributed synchronisation control of unknown nonlinear systems with an active leader,” Int. J. of Control, Vol.95, No.5, pp. 1396-1408, 2022. https://doi.org/10.1080/00207179.2020.1856929
- [22] Z. Wu, F. Deng, B. Guo, C. Wu, and Q. Xiang, “Backstepping Active Disturbance Rejection Control for Lower Triangular Nonlinear Systems With Mismatched Stochastic Disturbances,” IEEE Trans. on Systems, Man, and Cybernetics: Systems, Vol.52, No.4, pp. 2688-2702, 2022. https://doi.org/10.1109/TSMC.2021.3050820
- [23] J. Zhang, P. Shi, Y. Xia, and H. Yang, “Discrete-Time Sliding Mode Control With Disturbance Rejection,” IEEE Trans. on Industrial Electronics, Vol.66, No.10, pp. 7967-7975, 2019. https://doi.org/10.1109/TIE.2018.2879309
- [24] J. She, M. Fang, Y. Ohyama, H. Hashimoto, and M. Wu, “Improving Disturbance-Rejection Performance Based on an Equivalent-Input-Disturbance Approach,” IEEE Trans. on Industrial Electronics, Vol.55, No.1, pp. 380-389, 2008. https://doi.org/10.1109/TIE.2007.905976
- [25] M. Li, J. She, Z. Liu et al., “A Modified Disturbance-Rejection Approach in Networked Control Systems Based on Adaptive Model Predictive Control and Equivalent-Input-Disturbance,” J. Adv. Comput. Intell. Intell. Inform., Vol.26 No.4, pp. 495-503, 2022. https://doi.org/10.20965/jaciii.2022.p0495
- [26] Y. Zhou, J. She, F. Wang, and M. Iwasaki, “Disturbance Rejection for Stewart Platform Based on Integration of Equivalent-Input- Disturbance and Sliding-Mode Control Methods,” IEEE/ASME Trans. on Mechatronics, Vol.28, No.4, pp. 2364-2374, 2023. https://doi.org/10.1109/TMECH.2023.3237135
- [27] Q. Mei, J. She, and Z. Liu, “Disturbance rejection and control system design based on a high-order equivalent-input-disturbance estimator,” J. of the Franklin Institute, Vol.358, No.16, pp. 8736-8753, 2021. https://doi.org/10.1016/j.jfranklin.2021.08.010
- [28] Z. Wang, J. She, Z. Liu, and M. Wu, “Modified Equivalent-Input-Disturbance Approach to Improving Disturbance-Rejection Performance,” IEEE Trans. on Industrial Electronics, Vol.69, No.1, pp. 673-683, 2022. https://doi.org/10.1109/TIE.2021.3053889
- [29] J. Hu and A. Lanzon, “Cooperative Adaptive Time-Varying Formation Tracking for Multiagent Systems with LQR Performance Index and Switching Directed Topologies,” 2018 IEEE Conf. on Decision and Control (CDC), pp. 5102-5107, 2018. https://doi.org/10.1109/CDC.2018.8619623
- [30] C. Mu, Q. Zhao, and C. Sun, “Optimal Model-Free Output Synchronization of Heterogeneous Multiagent Systems Under Switching Topologies,” IEEE Trans. on Industrial Electronics, Vol.67, No.12, pp. 10951-10964, 2020. https://doi.org/10.1109/TIE.2019.2958277
- [31] L. Ji, C. Wang, C. Zhang et al., “Optimal consensus model-free control for multiagent systems subject to input delays and switching topologies,” Information Sciences, Vol.589, pp. 497-515, 2022. https://doi.org/10.1016/j.ins.2021.12.125
- [32] W. He, X. Chen, M. Zhang et al., “Data-Driven Optimal Consensus Control for Switching Multiagent Systems via Joint Communication Graph,” IEEE Trans. on Industrial Informatics, Vol.20, No.4, pp. 5959-5968, 2024. https://doi.org/10.1109/TII.2023.3342881
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.