Research Paper:
Parameter-Free Interval Priority Weight Estimation Methods Based on Minimum Conceivable Ranges Under a Crisp Pairwise Comparison Matrix
Shigeaki Innan and Masahiro Inuiguchi

Osaka University
1-3 Machikaneyama, Toyonaka, Osaka 560-8531, Japan
Methods for interval priority weight estimation from a crisp pairwise comparison matrix were proposed in the interval analytic hierarchy process assuming the vagueness of human evaluation. The interval priority weights estimated by the conventional method do not reflect the intrinsic vagueness in the given pairwise comparison matrix (PCM). This paper proposes parameter-free methods based on minimal conceivable ranges for estimating interval priority weights from a crisp pairwise comparison matrix. The estimated interval priority weight vectors are required to satisfy (1) the potential reproducibility, (2) the normality, and (3) the preservation of the perfect consistent data. Estimation methods of interval priority weights are proposed based on the minimum possible range. We show those proposed methods satisfy the required three properties. The estimation problem of interval priority weights potentially has multiple solutions with which the associated interval PCMs are identical to one another. To make the further investigation simpler, we use an interval priority weight vector among multiple solutions such that the sum of the center values of interval priority weights is one. We compare the estimation methods of interval priority weights from the viewpoint of estimation accuracy by numerical experiments. Namely, by generating crisp pairwise comparison matrices randomly under true interval PCMs, we evaluate the accuracies of the estimated interval priority weight vectors by comparing the true interval priority weight vectors.
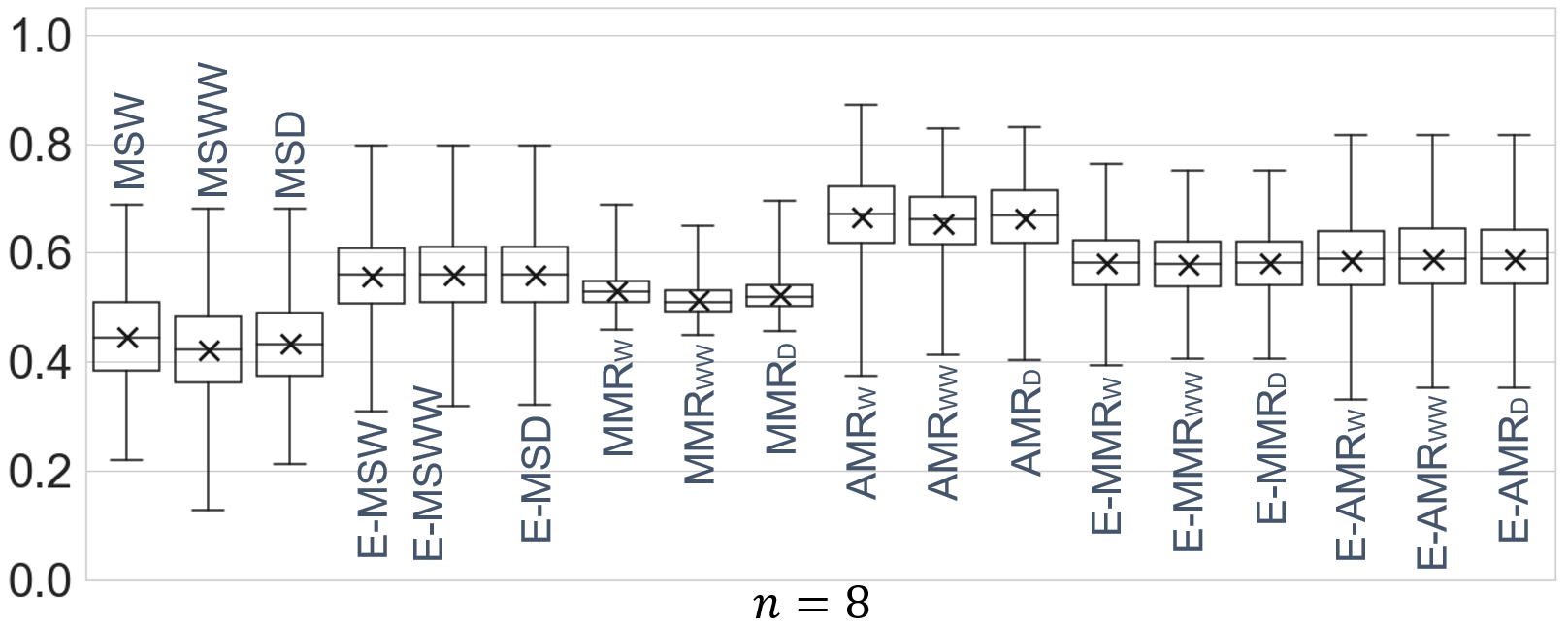
Estimation accuracy scores of various methods
- [1] S. Greco, M. Ehrgott, and J. Figueira (Eds.), “Multiple Criteria Decision Analysis: State of the Art Surveys, Second Edition,” Springer, New York, 2016.
- [2] S. Corrente, S. Greco, M. Kadziński, and R. Słowiński, “Robust Ordinal Regression in Preference Learning and Ranking,” Machine Learning, Vol.93, No.2, pp. 381-422, 2013. https://doi.org/10.1007/s10994-013-5365-4
- [3] S. A. Arcidiacono, S. Corrente, and S. Greco, “As Simple as Possible but not Simpler in Multiple Criteria Decision Aiding: The Robust-stochastic Level Dependent Choquet Integral Approach,” European J. of Operational Research, Vol.280, pp. 988-1007, 2020. https://doi.org/10.1016/j.ejor.2019.07.065
- [4] Z. Ru, J. Liu, M. Kadziński, and X. Liao, “Probabilistic Ordinal Regression Methods for Multiple Criteria Sorting Admitting Certain and Uncertain Preferences,” European J. of Operational Research, Vol.311, pp. 596-616, 2023. https://doi.org/10.1016/j.ejor.2023.05.007
- [5] T. L. Saaty, “The Analytic Hierarchy Process,” McGraw-Hill, New York, 1980.
- [6] T. L. Saaty and C. G. Vargas, “Comparison of Eigenvalue, Logarithmic Least Squares and Least Squares Methods in Estimating Ratios,” Mathematical Modelling, Vol.5, pp. 309-324, 1984. https://doi.org/10.1016/0270-0255(84)90008-3
- [7] A. Arbel, “Approximate Articulation of Preference and Priority Derivation,” European J. of Operational Research, Vol.43, pp. 317-326, 1989. https://doi.org/10.1016/0377-2217(89)90231-2
- [8] A. Arbel and L. G. Vargas, “Preference Simulation and Preference Programming: Robustness Issues in Priority Derivation,” European J. of Operational Research, Vol.69, pp. 200-209, 1993. https://doi.org/10.1016/0377-2217(93)90164-I
- [9] A. A. Salo, “Inconsistency Analysis by Approximately Specified Priorities,” Mathematical and Computer Modelling, Vol.17, Nos.4-5, pp. 123-133, 1993. https://doi.org/10.1016/0895-7177(93)90181-W
- [10] A. Arbel and L. G. Vargas, “Interval Judgements and Euclidean Centers,” Mathematical and Computer Modelling, Vol.46, Nos.7-8, pp. 976-984, 2007.
- [11] M. Kress, “Approximate Articulation of Preference and Priority Deviation: A Comment,” European J. of Operational Research, Vol.52, pp. 382-383, 1991. https://doi.org/10.1016/0377-2217(91)90174-T
- [12] R. Islam, M. P. Biswal, and S. S. Alam, “Preference Programming and Inconsistent Interval Judgements,” European J. of Operational Research, Vol.97, pp. 53-62, 1997. https://doi.org/10.1016/S0377-2217(95)00377-0
- [13] A. Salo and A. Punkka, “Rank Inclusion in Criteria Hierarchies,” European J. of Operational Research, Vol.163, pp. 338-356, 2005. https://doi.org/10.1016/j.ejor.2003.10.014
- [14] S. Siraj, L. Mikhailov, and J. A. Keane, “Enumerating All Spanning Trees for Pairwise Comparisons,” Computers & Operations Research, Vol.39, No.2, pp. 191-199, 2012. https://doi.org/10.1016/j.cor.2011.03.010
- [15] M. Lundy, S. Siraj, and S. Greco, “The Mathematical Equivalence of the “Spanning Tree” and Row Geometric Mean Preference Vectors and Its Implications for Preference Analysis,” European J. of Operational Research, Vol.257, pp. 197-208, 2017. https://doi.org/10.1016/j.ejor.2016.07.042
- [16] J. Mazurek and K. Kułakowski, “On the Derivation of Weights from Incomplete Pairwise Comparisons Matrices via Spanning Trees with Crisp and Fuzzy Confidence Levels,” Int. J. of Approximate Reasoning, Vol.150, pp. 247-257, 2022. https://doi.org/10.1016/j.ijar.2022.08.014
- [17] K. Sugihara and H. Tanaka, “Interval Evaluations in the Analytic Hierarchy Process by Possibilistic Analysis,” Computational Intelligence, Vol.17, pp. 567-579, 2001. https://doi.org/10.1111/0824-7935.00163
- [18] K. Sugihara, H. Ishii, and H. Tanaka, “Interval Priorities in AHP by Interval Regression Analysis,” European J. of Operational Research, Vol.158, No.3, pp. 745-754, 2004. https://doi.org/10.1016/S0377-2217(03)00418-1
- [19] Y.-M. Wang and T. M. S. Elhag, “A Goal Programming Method for Obtaining Interval Weights from an Interval Comparison Matrix,” European J. of Operational Research, Vol.177, pp. 458-471, 2007. https://doi.org/10.1016/j.ejor.2005.10.066
- [20] L. Mikhailov, “A Fuzzy Approach to Deriving Priorities from Interval Pairwise Comparison Judgments,” European J. of Operational Research, Vol.159, pp. 687-704, 2004. https://doi.org/10.1016/S0377-2217(03)00432-6
- [21] T. Entani and K. Sugihara, “Uncertainty index based interval assignment by Interval AHP,” European J. of Operational Research, Vol.219, pp. 379-385, 2012. https://doi.org/10.1016/j.ejor.2012.01.010
- [22] T. Entani and M. Inuiguchi, “Pairwise Comparison Based Interval Analysis for Group Decision Aiding with Multiple Criteria,” Fuzzy Sets and Systems, Vol.274, pp. 79-96, 2015. https://doi.org/10.1016/j.fss.2015.03.001
- [23] K. W. Li, Z.-J. Wang, and X. Tong, “Acceptability Analysis and Priority Weight Elicitation for Interval Multiplicative Comparison Matrices,” European J. of Operational Research, Vol.250, pp. 628-638, 2016. https://doi.org/10.1016/j.ejor.2015.09.010
- [24] B. Cavallo and M. Brunelli, “A General Unified Framework for Interval Pairwise Comparison Matrices,” Int. J. of Approximate Reasoning, Vol.93, pp. 178-198, 2018. https://doi.org/10.1016/j.ijar.2017.11.002
- [25] T. Kuo, “Interval Multiplicative Pairwise Comparison Matrix: Consistency, Indeterminacy and Normality,” Information Sciences, Vol.517, pp. 244-253, 2020. https://doi.org/10.1016/j.ins.2019.12.066
- [26] P. Grošelj and G. Dolinar, “Group AHP Framework Based on Geometric Standard Deviation and Interval Group Pairwise Comparisons,” Information Sciences, Vol.626, pp. 370-389, 2023. https://doi.org/10.1016/j.ins.2023.01.034
- [27] P. J. M. van Laarhoven and W. Pedrycz, “A Fuzzy Extension of Saaty’s Priority Theory,” Fuzzy Sets and Systems, Vol.11, pp. 229-241, 1983. https://doi.org/10.1016/S0165-0114(83)80082-7
- [28] J. J. Buckley, “Fuzzy Hierarchical Analysis,” Fuzzy Sets and Systems, Vol.17, pp. 233-247, 1985. https://doi.org/10.1016/0165-0114(85)90090-9
- [29] J. J. Buckley, T. Feuring, and Y. Hayashi, “Fuzzy Hierarchical Analysis Revisited,” European J. of Operational Research, Vol.129, pp. 48-64, 2001. https://doi.org/10.1016/S0377-2217(99)00405-1
- [30] R. Csutora and J. J. Buckley, “Fuzzy Hierarchical Analysis: The Lambda-max Method,” Fuzzy Sets and Systems, Vol.120, pp. 181-195, 2001. https://doi.org/10.1016/S0165-0114(99)00155-4
- [31] Y.-M. Wang, T. M. S. Elhag, and Z. Hua, “A Modified Fuzzy Logarithmic Least Squares Method for Fuzzy Analytic Hierarchy Process,” Fuzzy Sets and Systems, Vol.157, pp. 3055-3071, 2006. https://doi.org/10.1016/j.fss.2006.08.010
- [32] J. Ramík and R. Perzina, “A Method for Solving Fuzzy Multicriteria Decision Problems with Dependent Criteria,” Fuzzy Optimization and Decision Making, Vol.9, No.2, pp. 123-141, 2010. https://doi.org/10.1007/s10700-010-9078-x
- [33] L. Mikhailov and P. Tsvetinov, “Evaluation of Services Using a Fuzzy Analytic Hierarchy Process,” Applied Soft Computing, Vol.5, pp. 23-33, 2004. https://doi.org/10.1016/j.asoc.2004.04.001
- [34] E. Dopazo, S. C. K. Lui, and J. Guisse, “A Parametric Model for Determining Consensus Priority Vectors from Fuzzy Comparison Matrices,” Fuzzy Sets and Systems, Vol.246, pp. 49-61, 2014. https://doi.org/10.1016/j.fss.2013.07.022
- [35] Z. Zhang and W. Pedrycz, “Analysis of Acceptably Multiplicative Consistency and Consensus for Incomplete Interval-Valued Intuitionistic Fuzzy Preference Relations,” IEEE Trans. on Fuzzy Systems, Vol.30, No.2, pp. 486-499, 2022. https://doi.org/10.1109/TFUZZ.2020.3041164
- [36] J. Ramík, “Deriving Priority Vector from Pairwise Comparisons Matrix with Fuzzy Elements by Solving Optimization Problem,” OPSEARCH, Vol.60, pp. 1045-1062, 2023. https://doi.org/10.1007/s12597-023-00641-4
- [37] S. Innan and M. Inuiguchi, “Improvement of Interval Weight Estimation in Interval AHP,” Proc. of 2016 Joint 8th Int. Conf. on Soft Computing and Intelligent Systems and 2016 17th Int. Symposium on Advanced Intelligent Systems (SCIS&ISIS 2016), pp. 552-557, 2016. https://doi.org/10.1109/SCIS-ISIS.2016.0121
- [38] M. Inuiguchi and S. Innan, “Non-Parametric Interval Weight Estimation Methods from a Crisp Pairwise Comparison Matrix,” Proc. of Joint 17th World Congress of Int. Fuzzy Systems Association and 9th Int. Conf. on Soft Computing and Intelligent Systems, 2017. https://doi.org/10.1109/IFSA-SCIS.2017.8023261
- [39] M. Inuiguchi and S. Innan, “Improving Interval Weight Estimations in Interval AHP by Relaxations,” J. Adv. Comput. Intell. Intell. Inform., Vol.21, No.7, pp. 1135-1143, 2017. https://doi.org/10.20965/jaciii.2017.p1135
- [40] M. Yamaguchi and M. Inuiguchi, “Estimation Methods of Interval Weights Centered at Geometric Mean from a Pairwise Comparison Matrix,” Proc. of 2018 Joint 10th Int. Conf. on Soft Computing and Intelligent Systems and 19th Int. Symposium on Advanced Intelligent Systems (SCIS&ISIS 2018), pp. 1382-1387, 2018. https://doi.org/10.1109/SCIS-ISIS.2018.00215
- [41] M. Inuiguchi and I. Torisu, “The Advantage of Interval Weight Estimation over the Conventional Weight Estimation in AHP in Ranking Alternatives,” Proc. of Integrated Uncertainty in Knowledge Modelling and Decision Making: 8th Int. Symposium (IUKM 2020), LNCS, Vol.12482, pp. 38-39, 2020. https://doi.org/10.1007/978-3-030-62509-2_4
- [42] M. Inuiguchi, A. Hayashi, and S. Innan, “Comparing the Ranking Accuracies among Interval Weight Estimation Methods at the Standard, Minimum and Maximum Solutions under Crisp Pairwise Comparison Matrices,” Proc. of 2022 Joint 12th Int. Conf. on Soft Computing and Intelligent Systems and 23rd Int. Symposium on Advanced Intelligent Systems (SCIS&ISIS 2022), 2022. https://doi.org/10.1109/SCISISIS55246.2022.10002032
- [43] Y. Kato, “Reikai AHP: Kiso to Oyo (Analysis of AHP: Foundation and Applications),” Minerva Shobo, Kyoto, 2013 (in Japanese).
- [44] H. Tanaka, K. Sugihara, and Y. Maeda, “Non-Additive Measures by Interval Probability Functions,” Information Sciences, Vol.164, pp. 209-227, 2004. https://doi.org/10.1016/j.ins.2003.06.001
- [45] M. Inuiguchi, “Non-Uniqueness of Interval Weight Vector to Consistent Interval Pairwise Comparison Matrix and Logarithmic Estimation Methods,” Proc. of Integrated Uncertainty in Knowledge Modelling and Decision Makin (IUKM 2016), LNCS, Vol.9978, pp. 39-50, 2016. https://doi.org/10.1007/978-3-319-49046-5_4
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.