Research Paper:
Three Fuzzy c-Shapes Clustering Algorithms for Series Data
Mizuki Fujita and Yuchi Kanzawa

Shibaura Institute of Technology
3-7-5 Toyosu, Koto-ku, Tokyo 135-8548, Japan
Various fuzzy clustering algorithms have been proposed for vectorial data. However, most of these methods have not been applied to series data. This study presents three fuzzy clustering algorithms for series data based on shape-based distances. The first algorithm involves Shannon entropy regularization of the k-shape objective function. The second algorithm is similar to the revised Bezdek-type fuzzy c-means algorithm obtained by replacing the membership of the hard c-means objective function with its power. The third algorithm involves Tsallis entropy regularization of the objective function of the second algorithm. Theoretical observations revealed that the third algorithm is a generalization of the first and second algorithms, which was validated by numerical experiments. Furthermore, numerical experiments were performed using 11 benchmark datasets to demonstrate that the third algorithm outperforms the others in terms of accuracy.
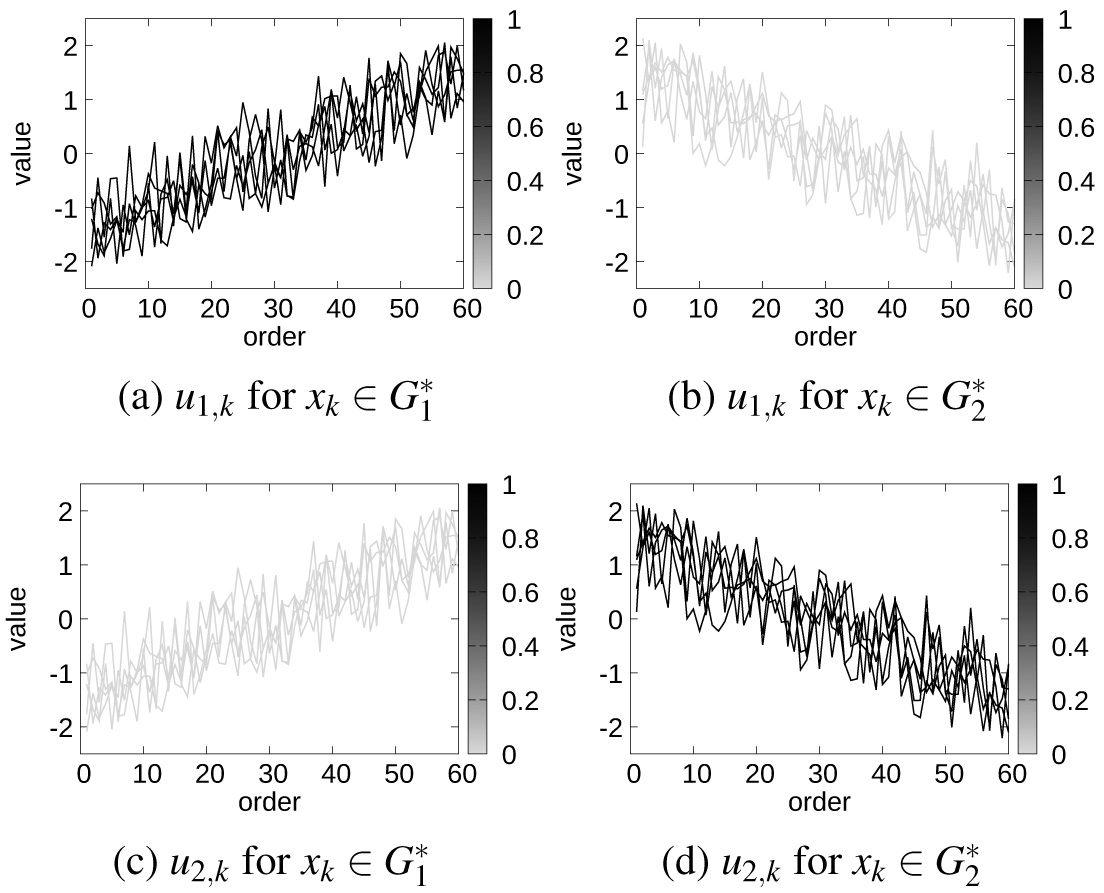
Memberships of the EFCSp approach
- [1] J. C. Bezdek, “Pattern Recognition with Fuzzy Objective Function Algorithms,” Springer New York, 1981. https://doi.org/10.1007/978-1-4757-0450-1
- [2] J. B. MacQueen, “Some methods for classification and analysis of multivariate observations,” Proc. of the 5th Berkeley Symp. Math. Stat. Prob., pp. 281-297, 1967.
- [3] S. Miyamoto and M. Mukaidono, “Fuzzy c-means as a regularization and maximum entropy approach,” Proc. of the 7th Int. Fuzzy Syst. Assoc. World Congr. (IFSA’97), pp. 86-92, 1997.
- [4] M. Ménard, V. Courboulay, and P.-A. Dardignac, “Possibilistic and Probabilistic Fuzzy Clustering: Unification Within the Framework of the Nonextensive Thermostatistics,” Pattern Recogn., Vol.36, No.6, pp. 1325-1342, 2003. https://doi.org/10.1016/S0031-3203(02)00049-3
- [5] J. Paparrizos and L. Gravano, “k-shape: Efficient and accurate clustering of time series,” ACM SIGMOD Record, Vol.45, No.1, pp. 69-76, 2015. https://doi.org/10.1145/2949741.2949758
- [6] F. Fahiman, J. C. Bezdek, S. M. Erfani, M. Palaniswami, and C. Leckie, “Fuzzy c-shape: A new algorithm for clustering finite time series waveforms,” Proc. of 2017 IEEE Int. Conf. on Fuzzy Syst. (FUZZ-IEEE), 2017. https://doi.org/10.1109/FUZZ-IEEE.2017.8015525
- [7] K. Honda, S. Oshio, and A. Notsu, “Fuzzy co-clustering induced by multinomial mixture models,” J. Adv. Comput. Intell. Intell. Inform., Vol.19, No.6, pp. 717-726, 2015. https://doi.org/10.20965/jaciii.2015.p0717
- [8] S. Miyamoto, H. Ichihashi, and K. Honda, “Algorithms for Fuzzy Clustering,” Springer Berlin, 2008. https://doi.org/10.1007/978-3-540-78737-2
- [9] C. Tsallis, “Possible Generalization of Boltzmann–Gibbs Statistics,” J. Statist. Phys., Vol.52, Nos.1-2, pp. 479-487, 1988. https://doi.org/10.1007/BF01016429
- [10] Y. Kanzawa and S. Miyamoto, “Generalization of Tsallis Entropy-Based Fuzzy c-Means Clustering and its Behavior at the Infinity Point,” J. Adv. Comput. Intell. Intell. Inform., Vol.26, No.6, pp. 884-892, 2022. https://doi.org/10.20965/jaciii.2022.p0884
- [11] H. A. Dau, E. Keogh, K. Kamgar, C.-C. M. Yeh, Y. Zhu, S. Gharghabi, C. A. Ratanamahatana, Y. Chen, B. Hu, N. Begum, A. Bagnall, A. Mueen, G. Batista, and Hexagon-ML, “The UCR Time Series Classification Archive.” https://www.cs.ucr.edu/eamonn/time_series_data_2018/ [Accessed December 12, 2021].
- [12] L. Hubert and P. Arabie, “Comparing partition,” J. Classif., Vol.2, pp. 193-218, 1985. https://doi.org/10.1007/BF01908075
- [13] F. Petitjean, A. Ketterlin, and P. Gançarski, “A global averaging method for dynamic time warping, with applications to clustering,” Pattern Recogn., Vol.44, No.3, pp. 678-693, 2011. https://doi.org/10.1016/j.patcog.2010.09.013
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.