Paper:
Trend Forecast of Shanghai Crude Oil Futures
Yutao Huang, Wenyu Yuan, Meiyu Wang, Wentao Gu†, and Linghong Zhang
Department of Statistics, School of Statistics and Mathematics, Zhejiang Gongshang University
18 Xuezheng Street, Xiasha Education Park, Hangzhou, Zhejiang 310018, China
†Corresponding author
The dominant position in crude oil pricing affects a country’s energy and economic security. We construct different time-series forecasting models to analyze the long-term trends of Shanghai crude oil futures and guide current price trading. First, we built a classic ARIMA model as the benchmark. It is a good choice for short-term investors but does not apply to long-term trend prediction. We propose an improved HW-Prophet model that can maximize its advantages in selecting and reconstructing mutation points and reduce the forecast error by approximately 22%. The Prophet model is then introduced into the prediction of futures price series, and the Haar wavelet and KS (HWKS) algorithm and sliding window are used to optimize the change-point selection of the Prophet model. Finally, we created different combinations of long short-term memory (LSTM) and HW-Prophet models based on residual correction and optimal weighting. The results showed that the combined residual correction method was unsuitable for the two single models in this study. Because the residual sequence predicted by the HW-Prophet model is similar to white noise, it is difficult for LSTM to learn the effective dynamic laws from it. By minimizing the error sum of squares to solve the optimal weight coefficients and combining the two models linearly, the prediction advantages of a single model in different intervals can be effectively transmitted, and the prediction accuracy is greatly improved. The HW-Prophet-LSTM combination model constructed in this study based on the optimal weight is currently one of the best models for predicting the long-term trends of Shanghai crude oil futures.
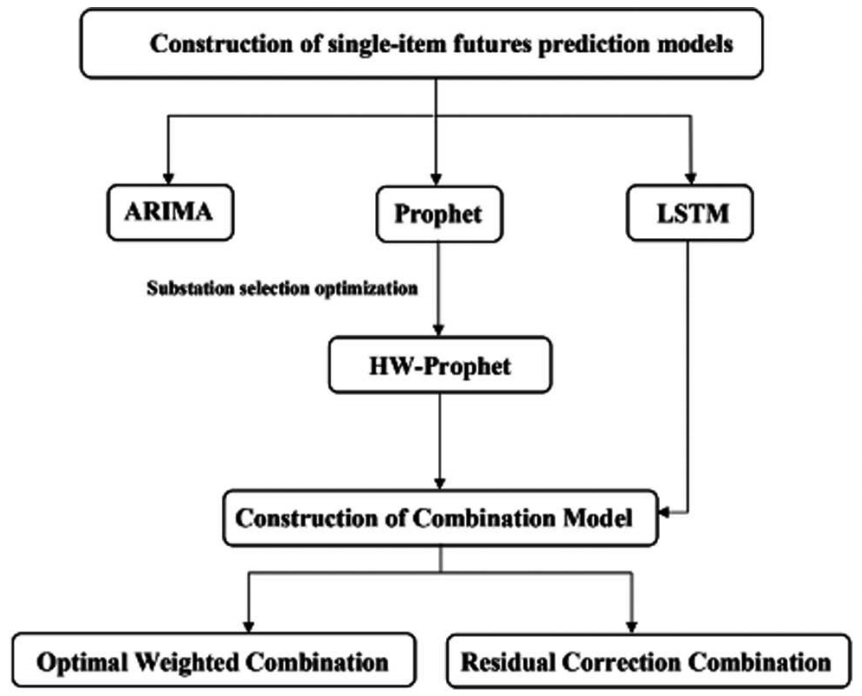
Flow chart construction of prediction models
- [1] H. Lai, “Passenger car consumption tax forecast based on time series Prophet model,” Tax Economic Research, No.1, pp. 34-39, 2020 (in Chinese).
- [2] K. Kim, “Financial time series forecasting using support vector machines,” Neurocomputing, Vol.55, Nos.1-2, pp. 307-319, 2003.
- [3] Y. LeCun, Y. Bengio, and G. Hinton, “Deep learning,” Nature, Vol.521, pp. 436-444, 2015.
- [4] J. Fan, H. Liu, and Y. Hu, “Soybean Futures Price Prediction Based on LSTM Deep Learning,” Price Monthly, No.2, pp. 7-15, 2021 (in Chinese).
- [5] C. Funk, “Forecasting the Real Price of Oil – Time-Variation and Forecast Combination,” Energy Economics, Vol.76, pp. 288-302, 2018.
- [6] H. Naser, “Estimating and forecasting the real prices of crude oil: A data rich model using a dynamic model averaging (DMA) approach,” Energy Economics, Vol.56, pp. 75-87, 2016.
- [7] G. Koop and D. Korobilis, “Forecasting Inflation Using Dynamic Model Averaging,” Int. Economic Review, Vol.53, No.3, pp. 867-886, 2012.
- [8] K. Drachal, “Forecasting spot oil price in a dynamic model averaging framework – Have the determinants changed over time?,” Energy Economics, Vol.60, pp. 35-46, 2016.
- [9] J. Quan, “Two-step testing procedure for price discovery role of futures prices,” J. of Futures Markets, Vol.12, No.2, pp. 139-149, 1992.
- [10] K. D. Garbade and W. L. Silber, “Price Movements and Price Discovery in the Futures and Cash Markets,” Review of Economics and Statistics, Vol.65, No.2, pp. 289-297, 1983.
- [11] A. Aue and L. Horváth, “Structural breaks in time series,” J. of Time Series Analysis, Vol.34, No.1, pp. 1-16, 2012.
- [12] L. Auret and C. Aldrich, “Change point detection in time series data with random forests,” Control Engineering Practice, Vol.18, No.8, pp. 990-1002, 2010.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.