Paper:
A Modified Disturbance-Rejection Approach in Networked Control Systems Based on Adaptive Model Predictive Control and Equivalent-Input-Disturbance
Meiliu Li*1,*2,*3, Jinhua She*4,†, Zhen-Tao Liu*1,*2,*3, Wangyong He*1*2*3, Feng Wang*1,*2,*3, Juan Zhao*1,*2,*3, and Yasuhiro Ohyama*4
*1School of Automation, China University of Geosciences
No.388 Lumo Road, Hongshan District, Wuhan 430074, China
*2Hubei Key Laboratory of Advanced Control and Intelligent Automation for Complex Systems
No.388 Lumo Road, Hongshan District, Wuhan 430074, China
*3Engineering Research Center of Intelligent Technology for Geo-Exploration, Ministry of Education
No.388 Lumo Road, Hongshan District, Wuhan 430074, China
*4School of Engineering, Tokyo University of Technology
1404-1 Katakura, Hachioji, Tokyo 192-0982, Japan
†Corresponding author
This paper presents an adaptive compensation control strategy for packet losses, time delays, and exogenous disturbances in a networked control system. The structure consists of five parts: a plant, a Luenberger observer, an equivalent-input-disturbance (EID) estimator, an adaptive model predictive controller (AMPC), and a network. The AMPC in the local main control room produces an adaptive tracking gain, which can ensure the effective tracking of the reference signal in the presence of uncertainty and time delays in the plant. The EID estimator at the local site compensates for packet losses and exogenous disturbances through an independently designed state observer and a low-pass filter. A practical application case results show the effectiveness of the presented method compared with the conventional EID approach.
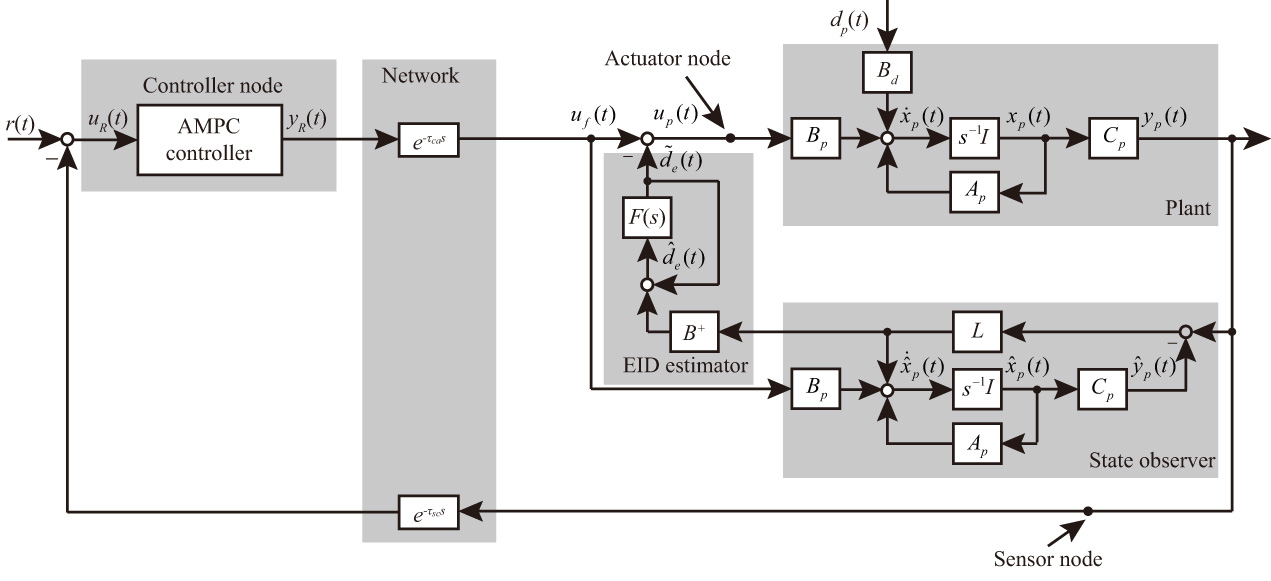
Structure of an AMPC-EID-based NCS
- [1] X. Zhang, Q. Han, and X. Yu, “Survey on Recent Advances in Networked Control Systems,” IEEE Trans. on Industrial Informatics, Vol.12, No.5, pp. 1740-1752, 2016.
- [2] H. Zhang, Z. Zhang, Z. Wang, and Q. Shan, “New Results on Stability and Stabilization of Networked Control Systems with Short Time-Varying Delay,” IEEE Trans. on Cybernetics, Vol.46, No.12, pp. 2772-2781, 2016.
- [3] L. Zhao, H. Xu, Y. Yuan, and H. Yang, “Stabilization for networked control systems subject to actuator saturation and network-induced delays,” Neurocomputing, Vol.267, pp. 354-361, 2017.
- [4] Y. Liu and C. Han, “Optimal Output Tracking Control and Stabilization of Networked Control Systems with Packet Losses,” J. of Systems Science and Complexity, Vol.34, pp. 602-617, 2021.
- [5] M. Li, J. She, Z. Liu et al., “Suppression of disturbances in networked control systems with time-varying delay based on equivalent-input-disturbance approach,” 45th Annual Conf. of the IEEE Industrial Electronics Society (IECON 2019), pp. 6957-6960, 2019.
- [6] M. Li, J. She, Z.-T. Liu et al., “An improved equivalent-input-disturbance method for uncertain networked control systems with packet losses and exogenous disturbances,” Actuators, Vol.10, No.10, Article No.263, 2021.
- [7] J. Ma, F. Pan, L. Zhou et al., “Modelling and stabilization of a wireless network control system with time delay,” Trans. of the Institute of Measurement and Control, Vol.40, No.2, pp. 640-646, 2016.
- [8] Z. Zhang, Z. Wang, X. Chen et al., “Improved results on BIBO stability and stabilization of networked control systems with short time-varying delays,” J. of the Franklin Institute, Vol.354, No.17, pp. 7699-7716, 2017.
- [9] H. Yan, Q. Yang, H. Zhang et al., “Distributed H∞ state estimation for a class of filtering networks with time-varying switching topologies and packet losses,” IEEE Trans. on Systems Man, and Cybernetics Systems, Vol.48, No.12, pp. 2047-2057, 2018.
- [10] J. Yan and Y. Xia, “Quantized control for networked control systems with packet dropout and unknown disturbances,” Information Sciences: an Int. J., Vol.354, No.C, pp. 86-100, 2016.
- [11] M. Li and Y. Chen, “Robust adaptive sliding mode control for switched networked control systems with disturbance and faults,” IEEE Trans. on Industrial Informatics, Vol.15, No.1, pp. 193-204, 2019.
- [12] T. Ogura, K. Kobayashi, H. Okada et al., “H∞ Control Design Considering Packet Loss as a Disturbance for Networked Control Systems,” IEICE Trans. on Fundamentals of Electronics, Communications and Computer Sciences, Vol.E100.A, No.2, pp. 353-360, 2017.
- [13] M. Li and Y. Chen, “Robust Tracking Control of Networked Control Systems with Communication Constraints and External Disturbance,” IEEE Trans. on Industrial Electronics, Vol.64, No.5, pp. 4037-4047, 2017.
- [14] T. Shi, P. Shi, and H. Zhang, “Model predictive control of distributed networked control systems with quantization and switching topology,” Int. J. of Robust and Nonlinear Control, Vol.30, No.12, pp. 4584-4599, 2020.
- [15] E. F. Camacho and C. Bordons, “Model Predictive Control,” Springer, 2007.
- [16] T. Wang, H. Gao, and J. Qiu, “A combined adaptive neural network and nonlinear model predictive control for multi-rate networked industrial process control,” IEEE Trans. on Neural Networks and Learning Systems, Vol.27, No.2, pp. 416-425, 2016.
- [17] J. Sun, J. Yang, S. Li et al., “Sampled-data-based event-triggered active disturbance rejection control for disturbed systems in networked environment,” IEEE Trans. on Cybernetics, Vol.49, No.2, pp. 556-566, 2019.
- [18] J. She, M. Fang, Y. Ohyama et al., “Improving disturbance-rejection performance based on an equivalent-input-disturbance approach,” IEEE Trans. on Industrial Electronics, Vol.55, No.1, pp. 380-389, 2008.
- [19] X. Yin, J. She, M. Wu et al., “Disturbance rejection and performance analysis for nonlinear systems based on nonlinear equivalent-input-disturbance approach,” Nonlinear Dynamics, Vol.100, pp. 3497-3511, 2020.
- [20] Y. Du, W. Cao, J. She et al., “Disturbance rejection and robustness of improved equivalent-input-disturbance-based system,” IEEE Trans. on Cybernetics, doi: 10.1109/TCYB.2021.3053597, 2021.
- [21] P. Yu, M. Wu, J. She et al., “An Improved Equivalent-Input-Disturbance Approach for Repetitive Control System with State Delay and Disturbance,” IEEE Trans. on Industrial Electronics, Vol.65, No.1, pp. 521-531, 2018.
- [22] M. Li, J. She, C.-K. Zhang et al., “Active disturbance rejection for time-varying state-delay systems based on equivalent-input-disturbance approach,” ISA Trans., Vol.108, pp. 69-77, 2021.
- [23] M. Li, J. She, Z.-T. Liu et al., “Suppression of packet losses and disturbances in networked control systems based on equivalent-input-disturbance approach,” IEEE Trans. on Cybernetics, doi: 10.1109/TCYB.2021.3080581, 2021.
- [24] M. Li, J. She, Z.-T. Liu et al., “Suppression of disturbances in networked control systems based on adaptive model predictive control and equivalent-input-disturbance approach,” Proc. of the 7th Int. Workshop on Advanced Computational Intelligence and Intelligent Informatics (IWACIII2021), Article No.T1-2-5, 2021.
- [25] D. W. C. Ho and G. Lu, “Robust stabilization for a class of discrete-time non-linear systems via output feedback: The unified LMI approach,” Int. J. of Control, Vol.76, No.2, pp. 105-115, 2003.
- [26] B. D. O. Anderson and J. B. Moore, “Optimal Control – Linear Quadratic Methods,” Prentice-Hall Int., Inc., 1989.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.