Paper:
Improved Tumor Image Estimation in X-Ray Fluoroscopic Images by Augmenting 4DCT Data for Radiotherapy
Takumi Shinohara*1, Kei Ichiji*2, Jiaoyang Wang*1, Noriyasu Homma*1,*2, Xiaoyong Zhang*2,*3, Norihiro Sugita*4, and Makoto Yoshizawa*5
*1Graduate School of Biomedical Engineering, Tohoku University
2-1 Seiryo-machi, Aoba-ku, Sendai, Miyagi 980-8575, Japan
*2Tohoku University Graduate School of Medicine
2-1 Seiryo-machi, Aoba-ku, Sendai, Miyagi 980-8575, Japan
*3National Institute of Technology, Sendai College
4-16-1 Ayashi-Chuo, Aoba-ku, Sendai, Miyagi 989-3128, Japan
*4Graduate School of Engineering, Tohoku University
6-6-05 Aramaki Aza Aoba, Aoba-ku, Sendai, Miyagi 980-8579, Japan
*5Center for Promotion of Innovation Strategy, Tohoku University
468-1 Aramaki Aza Aoba, Aoba-ku, Sendai, Miyagi 980-0845, Japan
Measurement of tumor position is important for the radiotherapy of lung tumors with respiratory motion. Although tumors can be observed using X-ray fluoroscopy during radiotherapy, it is often difficult to measure tumor position from X-ray image sequences accurately because of overlapping organs. To measure tumor position accurately, a method for extracting tumor intensities from X-ray image sequences using a hidden Markov model (HMM) has been proposed. However, the performance of tumor intensity extraction depends on limited knowledge regarding the tumor motion observed in the four-dimensional computed tomography (4DCT) data used to construct the HMM. In this study, we attempted to improve the performance of tumor intensity extraction by augmenting 4DCT data. The proposed method was tested using simulated datasets of X-ray image sequences. The experimental results indicated that the HMM using the augmentation method could improve tumor-tracking performance when the range of tumor movement during treatment differed from that in the 4DCT data.
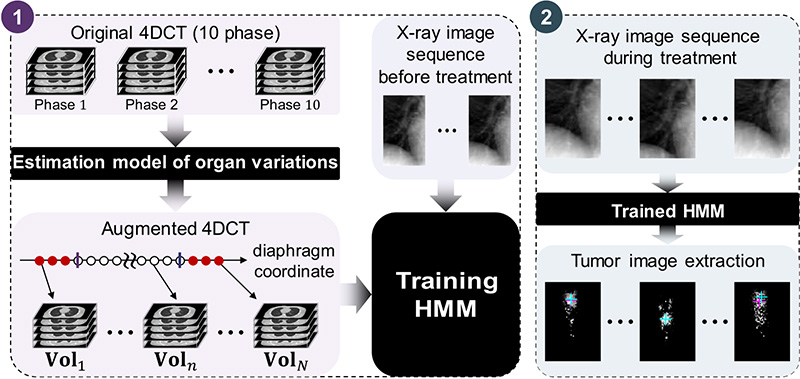
Process of tumor image extraction
- [1] P. Keall, P. Poulsen, and J. T. Booth, “See, Think, and Act: Real-Time Adaptive Radiotherapy,” Seminars in Radiation Oncology, Vol.29, No.3, pp. 228-235, 2019.
- [2] K. d. Bruin, M. Dahele, H. Mostafavi, B. J. Slotman, and W. F. Verbakel, “Markerless Real-Time 3-Dimensional kV Tracking of Lung Tumors During Free Breathing Stereotactic Radiation Therapy,” Advances in Radiation Oncology, Vol.6, No.4, Article No.100705, 2021.
- [3] X. Zhang, N. Homma, K. Ichiji, Y. Takai, and M. Yoshizawa, “Tracking tumor boundary in MV-EPID images without implanted markers: A feasibility study,” Medical Physics, Vol.42, No.5, pp. 2510-2523, 2015.
- [4] K. Ichiji, Y. Yoshida, N. Homma, X. Zhang, I. Bukovsky, Y. Takai, and M. Yoshizawa, “A key-point based real-time tracking of lung tumor in X-ray image sequence by using difference of Gaussians filtering and optical flow,” Physics in Medicine and Biology, Vol.63, No.18, Article No.185007, 2018.
- [5] P. J. Keall, G. S. Mageras, J. M. Balter, R. S. Emery, K. M. Forster, S. B. Jiang, J. M. Kapatoes, D. A. Low, M. J. Murphy, B. R. Murray, C. R. Ramsey, M. B. V. Herk, S. S. Vedam, J. W. Wong, and E. Yorke, “The Management of Respiratory Motion in Radiation Oncology Report of AAPM Task Group 76,” Medical Physics, Vol.33, No.10, pp. 3874-3900, 2006.
- [6] M. A. Hoggarth, J. Luce, F. Syeda, T. S. Bray, A. Block, S. Nagda, and J. C. Roeske, “Dual energy imaging using a clinical on-board imaging system,” Physics in Medicine and Biology, Vol.58, No.12, pp. 4331-4340, 2013.
- [7] R. Patel, J. Panfil, M. Campana, A. M. Block, M. M. Harkenrider, M. Surucu, and J. C. Roeske, “Markerless motion tracking of lung tumors using dual-energy fluoroscopy,” Medical Physics, Vol.42, No.1, pp. 254-262, 2014.
- [8] N. Shibusawa, K. Ichiji, Y. Yoshida, X. Zhang, N. Homma, Y. Takai, and M. Yoshizawa, “Target Extraction from X-ray Image Sequence by Using Gaussian Mixture Model for Lung Tumor Tracking,” IEICE Technical Report, Vol.114, No.482, pp. 277-282, 2015 (in Japanese).
- [9] M. Shindo, K. Ichiji, N. Homma, X. Zhang, S. Okuda, N. Sugita, S. Yamaki, Y. Takai, and M. Yoshizawa, “Hidden Markov model-based extraction of target objects in X-ray image sequence for lung radiation therapy,” IEEJ Trans. on Electronics, Information and Systems, Vol.140, No.1, pp. 49-60, 2020 (in Japanese).
- [10] S. Okuda, K. Ichiji, N. Homma, X. Zhang, and M. Yoshizawa, “Improvement of tumor visibility in X-ray image sequence by using hidden Markov model based on interpolated 4DCT,” SICE Tohoku 55th Aniversary Conf., 2019 (in Japanese).
- [11] M. Haytmyradov, H. Mostafavi, A. Wang, L. Zhu, M. Surucu, R. Patel, A. Ganguly, M. Richmond, R. Cassetta, M. M. Harkenrider, and J. C. Roeske, “Markerless tumor tracking using fast-kV switching dual-energy fluoroscopy on a benchtop system,” Medical Physics, Vol.46, No.7, pp. 3235-3244, 2019.
- [12] M. Lu, A. Wang, E. Shapiro, A. Shiroma, J. Zhang, J. Steiger, and J. Star-Lack, “Dual energy imaging with a dual-layer flat panel detector,” Proc. SPIE, Medical Imaging: Physics of Medical Imaging, Vol.10948, pp. 269-278, 2019.
- [13] J. Ge, L. Santanam, C. Noel, and P. J. Parikh, “Planning 4-dimensional computed tomography (4DCT) cannot adequately represent daily intrafractional motion of abdominal tumors,” Int. J. of Radiation Oncology Biology Physics, Vol.85, No.4, pp. 999-1005, 2013.
- [14] Q. Zhang, A. Pevsner, A. Hertanto, Y.-C. Hu, K. E. Rosenzweig, C. C. Ling, and G. S. Mageras, “A patient-specific respiratory model of anatomical motion for radiation treatment planning,” Medical Physics, Vol.34, No.12, pp. 4772-4781, 2007.
- [15] C. Yang, M. Guiney, P. Hughes, S. Leung, K. H. Liew, J. Matar, and G. Quong, “Use of digitally reconstructed radiographs in radiotherapy treatment planning and verification,” Australasian Radiology, Vol.44, No.4, pp. 439-443, 2000.
- [16] L. E. Baum, T. Petrie, G. Soules, and N. Weiss, “A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains,” Ann. Math. Statist., Vol.41, No.1, pp. 164-171, 1970.
- [17] A. J. Viterbi, “Error bounds for convolutional codes and an asymptotically optimal decoding algorithm,” IEEE Trans. Inf. Theory, Vol.13, No.2, pp. 260-269, 1967.
- [18] D. Zhou, H. Quan, D. Yan, S. Chen, A. Qin, C. Stanhope, M. Lachaine, and J. Liang, “A feasibility study of intrafractional tumor motion estimation based on 4D-CBCT using diaphragm as surrogate,” J. of Applied Clinical Medical Physics, Vol.19, No.5, pp. 525-531, 2018.
- [19] J. Thirion, “Image matching as a diffusion process: an analogy with Maxwell’s demons,” Medical Image Analysis, Vol.2, No.3, pp. 243-260, 1998.
- [20] I. T. Jollife and J. Cadima, “Principal component analysis: a review and recent developments,” Philosophical Trans. of the Royal Society A: Mathematical, Physical and Engineering Sciences, Vol.374, No.2065, doi: 10.1098/rsta.2015.0202, 2016.
- [21] W. Segars, M. Mahesh, T. Beck, E. Frey, and B. Tsui, “Realistic CT simulation using the 4D XCAT phantom,” Medical Physics, Vol.35, No.8, pp. 3800-3808, 2008.
- [22] Y. Suh, S. Dieterich, B. Cho, and P. J. Keall, “An analysis of thoracic and abdominal tumour motion for stereotactic body radiotherapy patients,” Physics in Medicine and Biology, Vol.53, No.13, pp. 3623-3640, 2008.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.